SOLUTION: In how many ways can nature select 6 students out of 17 to get the flu?

Algebra ->  Probability-and-statistics -> SOLUTION: In how many ways can nature select 6 students out of 17 to get the flu?      Log On


   

Question 851815: In how many ways can nature select 6 students out of 17 to get the flu?
Answer by josh_jordan(263) About Me  (Show Source):
You can put this solution on YOUR website!
This question is a combination question, because order does not matter. The order of the students doesn't matter, and there can be no repetition. So, the formula we will use to solve this, is:

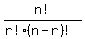
n%21%2F%28r%21%28n-r%29%21%29

n = the total number (17 in our problem)

r = the number taken (6 in our problem)

So, we will plug in 17 for n, and 6 for r in our formula:

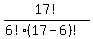
17%21%2F%286%21%2817-6%29%21%29

This means:



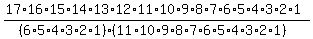
You can cross out any numbers that are in both the numerator and denominator. Doing so will give you:

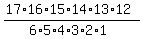
%2817%2A16%2A15%2A14%2A13%2A12%29%2F%286%2A5%2A4%2A3%2A2%2A1%29

Now, just multiply the numbers in the numerator and the numbers in the denominator, and then divide. So,

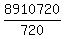8910720%2F720 ----->

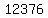12376. So, there are 12,376 ways nature can select 6 students out of 17 to get the flu.