Question 851043: So for homework i have been assigned "constructing triangles" on Khan Academy. The problem is: I cant understand it. It says a question like "Make a triangle with two 45 degree angles and one side length of 8" and then after spending a long time on making the triangle, i have to answer, "Are all triangles tat apply congruent?" I don't see any other triangles!!! I have to guess, and its a 50/50 chance to get it wrong! The present question says "How many triangles can we draw that have one angle measure equal to 45 degrees and one side of length 5?" Then the available answers are "None" "Only one" or "More than one." Please help me!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) In a triangle, congruent angles (with the same measure) are found opposite congruent sides (with the same length).
As a consequence, a triangle with two 45 degree angles is an isosceles triangle, which also has two equally long sides opposite those two equally wide angles.
In an isosceles triangle, the two equally long sides are called "legs".
The other side, adjacent to the two equally wide angles, is called the "base".
As your question is worded, the "one side" with a "length of 8" may be the base, or it may be one of the two equally long legs. If they asked for "exactly one side with a length of 8", that side would have to be the base, but here i have two choices, so I will draw two triangles that similar, but not congruent.

I could draw more triangles. Each would be congruent to one or the other triangle I drew above, but not all the triangles would be congruent.
NOTE:
Since two of the angles measure 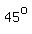 , the third angle must measure , the third angle must measure 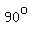 so those are right triangles. so those are right triangles.
I like to draw triangles sitting on a horizontal base, and I like my isosceles triangles sitting on their base.
However, I could draw these triangles sitting on one of their legs, because I like to draw right triangles sitting on one of their legs.
Drawing the triangles should not be difficult after you realize they are isosceles right triangles.

2) With one angle measuring 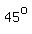 and one side of length 5", the possibilities are endless. and one side of length 5", the possibilities are endless.
I start with base AB measuring 5", and angle BAC measuring 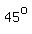 . .
(I draw ABC as a right triangle to get the 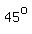 angle at A). angle at A).
The third vertex could be placed anywhere on the ray AC.
Triangles ABC, ABD, and ABE are some of the endless possibilities.

|
|
|