SOLUTION: Find the equation of the line that passes through (-8, 2) and (5, -7).

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: Find the equation of the line that passes through (-8, 2) and (5, -7).      Log On


   

Question 850858: Find the equation of the line that passes through (-8, 2) and (5, -7).
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
First we use the slope formula:

m = %28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29

where (x1,y1) = (-8, 2) 

and where (x2,y2) = (5, -7).

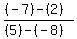m = %28%28-7%29-%282%29%29%2F%28%285%29-%28-8%29%29

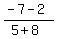m = %28-7-2%29%2F%285%2B8%29

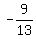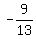m = %28-9%29%2F13 = -9%2F13

Then we use the point-slope formula:

y - y1 = m(x - x1)

where (x1,y1) = (-8, 2)

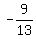and m = -9%2F13

y - y1 = m(x - x1)

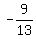y - 2 = -9%2F13(x - (-8))

y - 2 = -9%2F13(x + 8)

Multiply both sides by 13 to clear the fraction:

13(y - 2) = 13·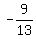-9%2F13(x + 8) 

13y - 26 = -9(x + 8)

13y - 26 = -9x - 72

9x + 13y = -46  < -- that's standard form.

or solve for y:

     13y = -9x - 46

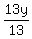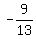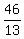     13y%2F13 = -9%2F13x - 46%2F13

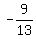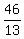     y = -9%2F13x - 46%2F13   < --- that's slope intercept form.

Edwin