I'll just tell you how.
1) Find the exact value of (Sin 130*)(cos 132*)+(cos 138*)(sin 132*)
Use the formula sin(A+B) =sin(A)cos(B)+cos(A)sin(B)
by substituting A=132°, B=138°, then use sin(270°) = -1
2) Simplify cos [a+pi/3]
Use cos(A+B) = cos(A)cos(B)-sin(A)sin(B)
with A=a and B= then use
then use  and
and 
3) Find the exact value of sin (60*+45*)
Use
sin(A+B) =sin(A)cos(B)+cos(A)sin(B)
with A=60° and B=45°
 and
and 
 and
and 
4) Find the exact value of cos [pi/3-pi/4]
Use cos(A-B) = cos(A)cos(B)+sin(A)sin(B)
with  and
and 
 and
and  and
and
 and
and 
5) Graph f(x) =-cos (3x+pi)
Write as f(x) = -cos[3(x+ )]
The five basic points of the graph of y=cos(x) are
(0,1),(
)]
The five basic points of the graph of y=cos(x) are
(0,1),( ,0),(
,0),( ,-1), (
,-1), ( ,0), (
,0), ( ,1)
The five basic points of the graph of y=-cos(x) are found by changing
the signs of the y-coordinates of the basic five points of the
graph of y=cos(x):
(0,-1),(
,1)
The five basic points of the graph of y=-cos(x) are found by changing
the signs of the y-coordinates of the basic five points of the
graph of y=cos(x):
(0,-1),( ,0),(
,0),( ,1), (
,1), ( ,0), (
,0), ( ,-1)
The five basic points of the graph of y=-cos(3x) are found by dividing
the x-coordinates of the basic five points of the graph of y=-cos(x)
by 3:
(0,-1),(
,-1)
The five basic points of the graph of y=-cos(3x) are found by dividing
the x-coordinates of the basic five points of the graph of y=-cos(x)
by 3:
(0,-1),( ,0),(
,0),( ,1), (
,1), ( ,0), (
,0), ( ,-1)
The five basic points of the graph of y=-cos[3(x+
,-1)
The five basic points of the graph of y=-cos[3(x+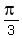 from the x-coordinates
of the basic five points of the graph of y=-cos(3x).
(
from the x-coordinates
of the basic five points of the graph of y=-cos(3x).
(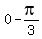 ,-1),(
,-1),(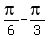 ,0),(
,0),(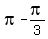 ,1), (
,1), (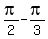 ,0), (
,0), (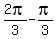 ,-1)
(
,-1)
(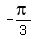 ,-1),(
,-1),(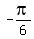 ,0),(
,0),( ,1), (
,1), ( ,0), (
,0), ( ,-1)
Plot those points and draw a curve through them.
,-1)
Plot those points and draw a curve through them.
6) Graph f(x) = cos[3(x+ )]
)]
That's the same problem as 5) except since it's positive,
you don't do the first step of changing the signs of the y-coordinates.
7) Find the phase shift and period for the function f(x)=3sin[x/2+pi]
Write as f(x) = 3sin( x+
x+ )
Then as f(x) = 3sin(
)
Then as f(x) = 3sin( x+
x+ )
Then as f(x) = 3sin(
)
Then as f(x) = 3sin(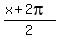 Then as f(x) = 3sin[
Then as f(x) = 3sin[ (x+
(x+ )
Then use the formula:
The period of y = Asin[B(x+C)] is
)
Then use the formula:
The period of y = Asin[B(x+C)] is 

 and its phase shift is
and its phase shift is 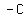 Edwin
Edwin