Question 850071: a manufacturer packages bolts in boxes containing 100 each. Each box of 100 bolts contains, on average, 5 defective bolts. the quality control staff randomly selects a box at the end of the day from an entire production run.
A. what is the probability, rounded to four decimal places, that the box will contain exactly 3 defective bolts
B. What is the probability, rounded to four decimal places that the box will contain at most 7 defective bolts?
c. what is the probability, rounded to four decimal places that the box will contain less than 4 defective bolts?
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
p = .05, n = 100
using TI Calculator
P(x=3) = The syntax is binompdf(n, p, x-value)= binompdf(100, .05,3)
Or
P =  (.05)^3(.95)^100 (.05)^3(.95)^100
Note: The probability of x successes in n trials is:
P (x)=  (p)^x(q)^(n-x) where p and q are the probabilities of success and failure respectively. (p)^x(q)^(n-x) where p and q are the probabilities of success and failure respectively.
In this case p = .05 & q = .95
 = = 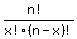
 = = 
B. What is the probability, rounded to four decimal places that the box will contain at most 7 defective bolts?
find P(x ≤ 7)= binomcdf(n, p, largest x-value) = binomcdf(100, .05, 7).
c. what is the probability, rounded to four decimal places that the box will contain less than 4 defective bolts?
find P(x < 4)= binomcdf(n, p, largest x-value) = binomcdf(100, .05, 3).
|
|
|