SOLUTION: a and b are quadrant 1 angles with cos(a)=15/17 and csc(b)=41/9 find sin (a+b). answer options are a. 185/697 b. 455/697 c. 528/697 d. 672/697 I receive the demonator of

We have to graph the two first quadrant angles, A and B.

Let's draw A first:

We are given this

 

We know that  or 

So we make the adjacent side, x, of A in the right triangle equal to the 
numerator of 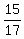, which is 15.  We make the hypotenuse, r,
of the right triangle equal to the denominator of the fraction,
which is 17. But we don't yet know y, so we put "y=? at first.
Like this:

 

Next we find y by the Pythagorean theorem

 r² = x²+y²
17² = 15²+y²
289 = 225+y²
 64 = y²
  8 = y 

So we can erase the question mark and put 8 in its place

 
 

Now let's draw to other first quadrant angle B :

We are given this

 

We know that  or 

So we make the hypotenuse of the right triangle r, equal to the 
numerator of 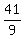, which is 41.  We make the opposite side
of the right triangle equal to the denominator of the fraction,
which is 9. But we don't yet know x, so we put "x=? at first.
Like this:

 

Next we find x by the Pythagorean theorem

  r² = x²+y²
 41² = x²+9²
1681 = x²+81
1600 = x²
  40 = x
  
So we can erase the question mark and put 40 in its place:

 

Now that we have x = adjacent, y = opposite, and r = hypotenuse for
both angles A and B, now we can proceed to find sin(A+B)  

Let's put both graphs here for convenience:

  

The identity for sin(A+B) is

sin(A+B) = sin(A)cos(B)+cos(A)sin(B)

sin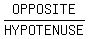(A) =  =  = 
cos(A) =  =  =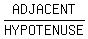 
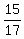sin(B) =  =  = 
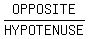cos(A) =  =  =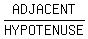 

Plug in:

sin(A+B) = sin(A)cos(B)+cos(A)sin(B)
sin(A+B) =  =  = 

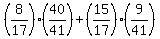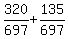Edwin