SOLUTION: Given a rational function with x-intercept at (0,0), two points at (1,1) and (-2,4), horizontal asymptote at y=2, and vertical asymptote at x=-1. Sketch the graph and write an equ

Algebra ->  Rational-functions -> SOLUTION: Given a rational function with x-intercept at (0,0), two points at (1,1) and (-2,4), horizontal asymptote at y=2, and vertical asymptote at x=-1. Sketch the graph and write an equ      Log On


   

Question 849547: Given a rational function with x-intercept at (0,0), two points at (1,1) and (-2,4), horizontal asymptote at y=2, and vertical asymptote at x=-1. Sketch the graph and write an equation for the function.
I have plotted the given points and asymptotes. I pretty much know how the graph is going, however I can't seem to figure out the equation. I know that the numerator should have 2x somewhere in it, but not sure where or what else goes with it. I know that the denominator is going to be x+1.
Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
the solution is:

(2x) / (x+1)

the graph that is generated looks like this:

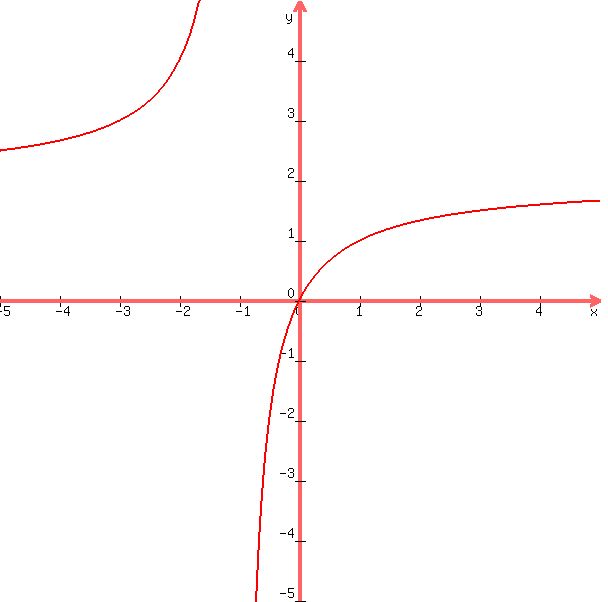
graph%28600%2C600%2C-5%2C5%2C-5%2C5%2C%282x%29%2F%28x%2B1%29%29

the table that could be generated looks like this: 

        x         y = (2x) / (x+1)

        -2             4
        -1             undefined
         0             0
         1             1
         2             4/3


since the vertical asymptote was at -1, the denominator of the graph had to be some for of x + 1 because then -1 + 1 = 0 and the graph is undefined at that point.

the numerator of the graph had to be the same level as the denominator, because then the graph has a horizontal asymptote at whatever level of y the numerator was at when the value of x goes to infinity.

a recommended method that i learned is that you divide the numerator and the denominator by the highest level exponent. This makes everything that is not important cancel out.

For example:

Assuming the numerator is 2x and the denominator is (x+1), and you want to find the horizontal asymptote, factor out the greatest exponent term.

2x factors out an x.

(x+1) factors out an x.

you are left with:

x * (2) / (x * (1 + 1/x)

now, as x goes to infinity, the numerator stays at 2 and the denominator stays at 1, so the limit of the expression as x goes to infinity is equal to 2.

the solution is part luck and part detective work in finding what the expression could be.

not sure if i would be successful every time, but it worked this time.

some tutorials on the web that may be helpful are:

http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut35_polyfun.htm

http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut40_ratgraph.htm