SOLUTION: Calculate the sum of all natural numbers from 100 to 200 both inclusive which are not divisible by 6

First we'll find the sum of all natural numbers from 100 to 200, inclusive.
Then we'll find the sum of all the multiples of 6 from 102 to 198, inclusive.
Then we'll subtract them.

All natural numbers from 100 to 200, inclusive.

That's the arithmetic sequence 100,101,102,103,...,200
with a1=100, d=1, and an=200


an = a1 + (n-1)d

To find the number of terms:

200 = 100 + (n-1)1
100 = n-1
101 = n

We use the sum formula

Sn = (a1 + an) 

S101 = 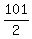(100 + 200) =  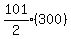= 15150

--------------------

The multiples of 6 from 102 to 198, inclusive, is the arithmetic
sequence 102,108,114,...,198, with a1=100, d=1, and an=200

To find the number of terms:

an = a1 + (n-1)d

198 = 102 + (n-1)6
198 = 102+6n-6 
198 = 96+6n
102 = 6n
 17 = n

We use the sum formula

Sn = (a1 + an) 

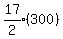S7 = (102 + 198) =  = 2550

Subtracting,  15150-2550 = 12600.

Answer = 12600.

Edwin