SOLUTION: In class we considered the rearrangement of the word 'ignominious'. a) How many rearrangements are possible if the first letter must be an 'i' and the last letter must be an 's'?

Algebra ->  Permutations -> SOLUTION: In class we considered the rearrangement of the word 'ignominious'. a) How many rearrangements are possible if the first letter must be an 'i' and the last letter must be an 's'?       Log On


   

Question 848964: In class we considered the rearrangement of the word 'ignominious'.
a) How many rearrangements are possible if the first letter must be an 'i' and the last letter must be an 's'?
b) How many rearrangements are possible if the first letter must be a constant? (Be careful - the calculations are not the same for all constants)
c) How many rearrangements are possible if the vowels must always be separated by atleast one constant?
d) How many rearrangements are possible if the constants must be kept together?
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
First learn that the letters that are not vowels are called "consonants",
not "constants".

"ignominious" has 6 vowels and 5 consonants.  There are 

3 indistinguishable i's 
2 indistinguishable o's
2 indistinguishable n's

In class we considered the rearrangement of the word 'ignominious'.
a) How many rearrangements are possible if the first letter must be an 'i' and the last letter must be an 's'?
i _ _ _ _ _ _ _ _ _ s

That's the number of distinguishable arrangements of the 9 other
letters "gnominiou", which has 2 indistinguishable n's, 2 indistinguishable
o's and 2 indistinguishable i's.

Answer: 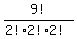9%21%2F%282%212%212%21%29 = 45360

b) How many rearrangements are possible if the first letter must be a consonant? (Be careful - the calculations are not the same for all consonants)
Case 1:  g comes first. g _ _ _ _ _ _ _ _ _ _ _ 

That's the number of distinguishable arrangements of the 10 other
letters "inominious", which has 3 indistinguishable i's, 2 indistinguishable
n's and 2 indistinguishable o's.

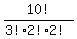10%21%2F%283%212%212%21%29 = 151200 ways

Case 2:  n comes first. n _ _ _ _ _ _ _ _ _ _ _ 

That's the number of distinguishable arrangements of the 10 other
letters "igominious", which has 3 indistinguishable i's, and 2 indistinguishable o's

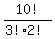10%21%2F%283%212%21%29 = 302400 ways

Case 3. m comes first.  Same as case 1, which was 151200
Case 4. s comes first.  Same as case 1, which was 151200


3×151200 + 302400 = 756000

c) How many rearrangements are possible if the vowels must always be separated by atleast one consonant?
Since we have 6 vowels and only 5 consonants, the only 
configuration possible is to alternate them like this:

VCVCVCVCVCV

We can place the 6 vowels distinguishably 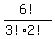6%21%2F%283%212%21%29 ways,
since the 3 i's are indistinguishable and the 2 o's are 
indistinguishable.

For each way we can place the 6 vowels, we can place the 5
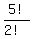consonants distinguishably in 5%21%2F%282%21%29 ways since the 2 n's 
are indistinguishable.

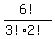
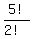So that's 6%21%2F%283%212%21%29%22%D7%225%21%2F%282%21%29 = 60×60 = 3600

d) How many rearrangements are possible if the consonants must be kept together?
There are 7 ways the 5 consonants can come together

1. CCCCCVVVVVV
2. VCCCCCVVVVV
3. VVCCCCCVVVV
4. VVVCCCCCVVV
5. VVVVCCCCCVV
6. VVVVVCCCCCV
7. VVVVVVCCCCC

Since the number of ways to place the 11 letters distinguishably 
in any given configuration of constants and vowels is the same as in
any other given configuration, we can just use the 3600 ways from part
(c) and multiply it by 7.

Answer 3600×7 = 25200

Edwin