|
Question 8488: Please help me. I have no idea what they want.
5. Put the following in turning point form (y = a(x-h)^2+k) and give the vertex and y-intercept.
a) 
c) 
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! While I'm familiar with the form:  , I was not aware that this form was called the turning point form...you learn something new every day! , I was not aware that this form was called the turning point form...you learn something new every day!
Anyway, putting your quadratic equations in this form you can quickly identify the location of the vertex of the parabola and other features.
So, step 1, get the quadratics into the "turning point" form, 
a)  You will need to "complete the square". This is a process by which you can write any general quadratic function You will need to "complete the square". This is a process by which you can write any general quadratic function  in the form in the form  where the vertex of its graph can be identified. Heres how: where the vertex of its graph can be identified. Heres how:
Isolate the x-terms by subtracting 3 from both sides:

Add the square of one half the x-coefficient. That's 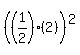 = 1 = 1
 Factor the trinomial as the square of a binomial. Factor the trinomial as the square of a binomial.
 now add 2 to both sides. now add 2 to both sides.
 Here's your quadratic in "turning point" form, Here's your quadratic in "turning point" form,  . .
The coordinates of the vertex are at: (h, k)
In this case, h = -1 and k = 2, so the vertex is located at (-1, 2)
To find the y-intercept, just set x = 0 in the original equation and solve for y.



The y-intercept is located at: (0, 3)
Try this on problem c)
|
|
|
| |