Question 8485: I am confused concerning inequalities involving absolute value. Could you help me with the problem |3x+7|<7?
Thank you
Found 2 solutions by prince_abubu, khwang:
Answer by prince_abubu(198)   (Show Source): (Show Source):
You can put this solution on YOUR website! When you see an inequality of this form, you must split it into 2 different inequalities - one being exactly what you have, (Case I) except take out the absolute value signs, and the other, (Case II) also taking out the absolute value signs, however, altering the signs of the terms that were inside the absolute value.
Case I - Problem as is - just take out the absolute value signs:
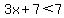 <------ You'd solve this as if the < were an = sign, except, keep in mind that it really is a <------ You'd solve this as if the < were an = sign, except, keep in mind that it really is a
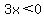 <---- subtract 7 from both sides. <---- subtract 7 from both sides.
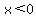 <---- divide by 3 on both sides. <---- divide by 3 on both sides.
--------------------------------------------------
Case II - Flip the signs of the terms inside absolute value; get rid of absolute value
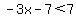 <-------- Start here <-------- Start here
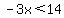 <------- Add 7 to both sides <------- Add 7 to both sides
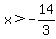 <------ Divide by -3 on both sides. Notice that the direction of your inequality CHANGED. This is due to dividing both sides by a negative number. It's a rule to flip inequality when you divide (or multiply) by a negative number. <------ Divide by -3 on both sides. Notice that the direction of your inequality CHANGED. This is due to dividing both sides by a negative number. It's a rule to flip inequality when you divide (or multiply) by a negative number.
So your answer is x > -14/3 and x < 0. Actually, when you put those together it's -14/3 < x < 0 because x lies between -14/3 and 0, but does not include those two values.
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solve: |3x+7|<7
A direct way to solve |ax-b| < c if a > 0 and c > 0
by converting it to -c < ax-b < c
or equivalently (b-c)/a < x < (b+c)/a
Here, a =3, b = -7, c = 7,
So, -14/3 < x < 0 or the interval (-14/3, 0)
Kenny
|
|
|