I have a question that states: Find the center
and radius of the circle with the given equation:
(x - 4)² + (y + 8)² = 9. How do I work this?
By memorizing the standard form of a circle, knowing
how to compare a given standard form to it, and
how to pick out the center and the radius:
Rule:
The standard form of a circle is
(x - h)² + (y - k)² = r²
with center (h,k) and radius r.
So compare your equation:
(x - 4)² + (y + 8)² = 9 to
(x - h)² + (y - k)² = r²
and you can see that
-h = -4 or h = 4,
-k = +8 or k = -8,
r² = 9 so r = 3
So the center is (h,k) = (4,-8) and the radius is r = 3.
-------------------------------------------
You don't need to check it, but let's do it anyway,
so you'll know why it's true and learn something
about the equation of a circle:
Draw the circle with center (4,-8) and radius = 3
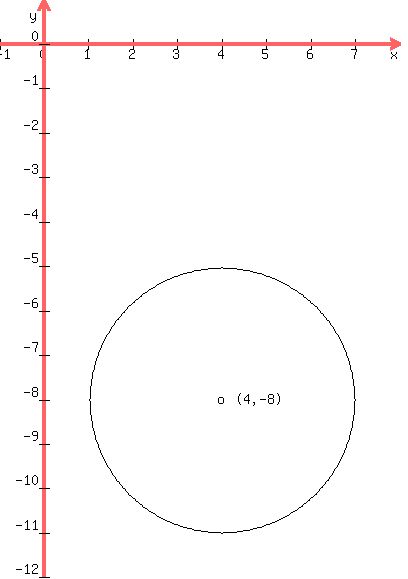The left-most point of the circle should be 3 units left
of the center or (1,-8).
Let's see if that satisfies the
equation
(x - 4)² + (y + 8)² = 9
(1 - 4)² + (-8 + 8) = 9
(-3)² + 0² = 9
9 + 0 = 9
9 = 9
Yes it does.
The upper-most point of the circle should be 3 units above
the center or (4,-5).
Let's see if that satisfies the
equation
(x - 4)² + (y + 8)² = 9
(4 - 4)² + (-5 + 8) = 9
(0)² + (-3)² = 9
0 + 9 = 9
9 = 9
Yes it does.
The right-most point of the circle should be 3 units right
of the center or (7,-8).
Let's see if that satisfies the
equation
(x - 4)² + (y + 8)² = 9
(7 - 4)² + (-8 + 8) = 9
(3)² + 0² = 9
9 + 0 = 9
9 = 9
Yes it does.
The lowest point of the circle should be 3 units below
of the center or (4,-11).
Let's see if that satisfies the
equation
(x - 4)² + (y + 8)² = 9
(4 - 4)² + (-11 + 8) = 9
(0)² + (-3)² = 9
0 + 9 = 9
9 = 9
Yes it does. So we know the center is (4,-8) and the radius
is 3.
Edwin
