Question 847401: Multiplying and simplifying radical expressions. Simplify by factoring. assume that all variables in a radicand represent positive real numbers and no radicands involve negative quantities raised to even powers.
x to the 8th power y to the 9th power inside a square root.
How do I solve this?
Answer by josh_jordan(263)   (Show Source): (Show Source):
You can put this solution on YOUR website! 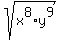
In order to simplify this root, all you have to do is divide each variable's exponent by 2. After you divide, if the result is a whole number with no remainder, that variable (along with it's result, will be placed outside the radical. If, after you divide, the result has a remainder, the variable, along with the quotient of the original power divided by 2, will be placed outside of the radical, and the variable and its remainder power will stay inside the radical.
So, with your particular problem, we will first divide the exponent of x (which is 8), by 2. 8/2 = 4. Because 4 is a whole number, and no remainder was left after we divided 4 by 2, we will place x^4 on the outside of the radical. So, right now, our expression looks like:
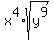
Next, we will divide the exponent of y (which is 9), by 2. 9/2 = 4 with a remainder of 1. So, we will place y^4 outside of the radical as well. Inside your radical, you will keep y^1 (or y) inside the radical, because our remainder after we divided, was 1. So, your final answer is:
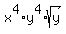
|
|
|