|
Question 847330: Find an equation of the circle that has center (4,-6) and passes through (-3,-4)
Found 2 solutions by josgarithmetic, MathLover1:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
You can put this solution on YOUR website! The value for the radius is, using the Distance Formula, 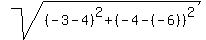 ; ;
Use knowledge of standard form for a circle.  and the center is (h,k). Your example uses h=4 and k=-6. Watch the signs carefully. and the center is (h,k). Your example uses h=4 and k=-6. Watch the signs carefully.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! The standard form of the equation for a circle is:
 where where 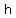 is the is the  coordinate of the center of the circle , coordinate of the center of the circle ,  is the is the  coordinate of the center of the circle, and coordinate of the center of the circle, and  is the radius of the circle . is the radius of the circle .
the circle that has center (4,-6) and passes through (-3,-4)
given:
the center of the circle at ( , ,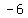 ) )
one point the circle passes through: ( , , ) )
The only thing we are missing to complete the equation for the circle is to know (if given) or derive (if not given),  , the radius of the circle. , the radius of the circle.
With the two points given: center ( , ,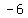 ) and circle passes through ( ) and circle passes through ( , , ) ; if we connect those two points together, that line will be equal the radius of the circle. ) ; if we connect those two points together, that line will be equal the radius of the circle.
To determine the radius, think about a right triangle that has as its " " side and " " side and " " side the rise and run difference between the two given points. And, knowing the Pythagorean theorem to determine the hypotenuse of a right triangle: " side the rise and run difference between the two given points. And, knowing the Pythagorean theorem to determine the hypotenuse of a right triangle:

We know that in in this instance the hypotenuse is equal to the radius of our circle, so we will substitute  for for  . .

If we take the square root of both sides of the previous equation we get:

To solve, you need:
 = the difference in the two = the difference in the two 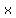 coordinates (from the two points given): coordinates (from the two points given):

and 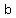 = the difference in the two y coordinates (from the two points given): = the difference in the two y coordinates (from the two points given):

then, 


To return to the original problem: determine the equation for the circle with the given center point and passing through the given point:
 which could be simplified to which could be simplified to

|
|
|
| |