Question 847225: Hi, I have not been able to get this question as I don't know where to start.
Thank you in advance for any help.
There is a diagram showing a sector oab of center o in which the angle aob is 120 degrees. There is a horizontal line drawn (ab) splitting the sector into a semicircle and a triangle.
i) Show that;
Area of sector oab/area of triangle oab = 4π/3√3
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! Area of the sector, based on it being 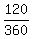 of the area of the circle of radius r, is of the area of the circle of radius r, is 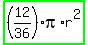 . .
The triangle with bottom side AB has two equal sides of r each. Note that this is two special triangles sharing a common side. If you split the triangle from the center point of the circle to the middle of AB, you have TWO 30-60-90 triangles. The bottom leg is (1/2)AB, the leg with endpoint at the circle center has length  , and hypotenuse is r. We know all this because we have a special right triangle. Drawing the picture of everything will help. With all this, first find the length AB, and then find the expression for the area of the central triangle (with the central angle 120 degrees). , and hypotenuse is r. We know all this because we have a special right triangle. Drawing the picture of everything will help. With all this, first find the length AB, and then find the expression for the area of the central triangle (with the central angle 120 degrees).
* ; ;
the algebra steps, not shown here, will give  ; the area for the 120 degree central triangle is ; the area for the 120 degree central triangle is 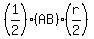 , half of base times height, , half of base times height,
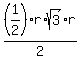
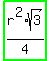 , the triangle's area. , the triangle's area.
The question asks, what is the ratio of the sector area to the area of triangle AOB. Form that ratio and simplify.
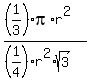


-------------
* A little more help from the Pythagorean Theorem relationship.
The "AB" is the geometry point notation for the measure of the segment, AB. The two special 30-60-90 triangles which make up the one central angled triangle have a leg of 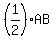 . The other "leg" is of length . The other "leg" is of length  , while the hypotenuse is r. , while the hypotenuse is r.
-
 and we want to solve for AB. and we want to solve for AB.







|
|
|