SOLUTION: Find the area of the triangle with vertices (0, 0), (5, 3) and (2, 6).

Algebra ->  Surface-area -> SOLUTION: Find the area of the triangle with vertices (0, 0), (5, 3) and (2, 6).      Log On


   

Question 846879: Find the area of the triangle with vertices (0, 0), (5, 3) and (2, 6).
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!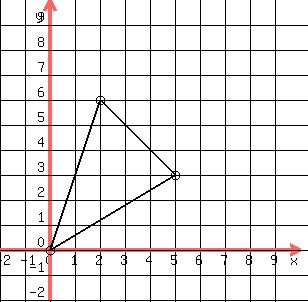

We need to find the altitude of the triangle.
Calculate the angle that the (0,0) to (5,3) line makes with the x-axis.
tan%28theta%29=3%2F5
theta=0.54042 radians
Calculate the angle that the (0,0) to (2,6) line makes with the x-axis.
tan%28theta%29=6%2F2
theta=1.24906 radians
So then the angle between the (2,6) line and the (5,3) line is
1.24906-0.54042=0.708626 radians
The sine of that angle and the hypotenuse would give us the altitude of the triangle.
The hypotenuse is the distance from (0,0) to (2,6)
H%5E2=%282-0%29%5E2%2B%286-0%29%5E2=40
H=sqrt%2840%29
So then,
A=sqrt%2840%29%2Asin%280.708626%29
The base of the triangle is the distance from (0,0) to (5,3),
B%5E2=5%5E2%2B3%5E2=34
B=sqrt%2834%29
So then the area of the triangle is,
A%5Bt%5D=%281%2F2%29A%2AB=%281%2F2%29sqrt%2840%29sqrt%2834%29sin%280.708626%29
A%5Bt%5D=%281%2F2%29A%2AB=%281%2F2%29sqrt%281360%29%2A0.650791
A%5Bt%5D=12