Question 846742: Perimeter is 116 area is 825 what are the dimensions
Answer by josh_jordan(263)   (Show Source): (Show Source):
You can put this solution on YOUR website! To find the dimensions of this rectangle, we need to know the formulas for the perimeter and area of rectangles:
Perimeter = 2L + 2W
Area = L x W
We are told the perimeter is 116 and the area is 825. So:
2L + 2W = 116
L x W = 825
Now that we have our equations, we can solve by rewriting our second equation in terms of either L or W and substituting that result into our first equation. Let's rewrite equation 2 in terms of L:
L = 825/W
Now, let's substitute 825/b for a in our first equation:
2(825/W) + 2W = 116
Multiply 2 by 825/W, which will give us
1650/W + 2W = 116
Now, we need to add 1650/W to 2W. To do this, multiply 1650/W by 1 and multiply 2W by W. add those results together and place in the numerator, and place "W" in the denominator:
 -----> ----->

Next, multiply both sides of the equation by W, giving us:

Now, we need to subtract 116W from both sides, giving us:

Rewrite in standard quadratic form:

Now, we will use the quadratic formula to solve for W:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=256 is greater than zero. That means that there are two solutions:  . .
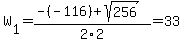

Quadratic expression 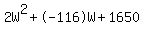 can be factored: can be factored:

Again, the answer is: 33, 25.
Here's your graph:
 |
Therefore, our width = 25 or 33
To find the length of our rectangle, we need to substitute 25 and 33 one at a time into one of our original equations. Let's use our original second equation, L x W = 825:
L x 25 = 825 ----->
L = 825/25 ----->
L = 33
So, one of the dimensions of our rectangle is: 33 x 25
Now, we need to find the other possible dimensions of our rectangle by substituting 33 for our width in L x W = 825:
L x 33 = 825 ----->
L = 825/33 ----->
L = 25
So the other possible dimensions of our rectangle are: 25 x 33
Therefore, our two possible sets of dimensions are: 33 x 25 OR 25 x 33
|
|
|