SOLUTION: The probability that an American household has a gun is 0.34 . Five American households are selected at random. (Report answers rounded to four decimal places. (a) What

Algebra ->  Probability-and-statistics -> SOLUTION: The probability that an American household has a gun is 0.34 . Five American households are selected at random. (Report answers rounded to four decimal places. (a) What       Log On


   

Question 846485: The probability that an American household has a gun is 0.34 . Five American households are selected at random. (Report answers rounded to four decimal places.

(a) What is the probability that exactly two of the five households have a gun?
Show work.

(b) What is the probability that none of the five households has a gun?
Show some work/explanation.

(c) What is the probability that all five of the households have a gun?
Show some work/explanation.

(d) What is the probability that at least one of the five households has a gun?
Show some work/explanation.





Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,

Note: The probability of x successes in n trials is: 

P = nCx* p%5Ex%2Aq%5E%28n-x%29 where p and q are the probabilities of success and failure 

p = .34,  n = 5

TI or long hand

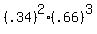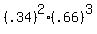
P(x=2) = binompdf(n, p, x-value)= binompdf(5, .34, 2)  Or 5C2 %28.34%29%5E2%2A%28.66%29%5E3 = 10%28.34%29%5E2%2A%28.66%29%5E3

P(x =0)= binompdf(n, p, x-value)= binompdf(5, .34, 0)  0r 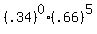%28.34%29%5E0%2A%28.66%29%5E5

P(x =5)= binompdf(n, p, x-value)= binompdf(5, .34, 5) 0r 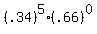%28.34%29%5E5%2A%28.66%29%5E0

P(x ≥ 1) = 1 -binomcdf(n, p, largest x-value) =  1 -binomcdf(5 .34. 0)