Graph the inequality.
3x + y < 5
First form the equation of the boundary line,
which is found by replacing the < by =
3x + y = 5
Draw this line by find the intercept (0,5) and (3,-4)
Draw the line solid, not dotted, because the inequality is
< and not <.
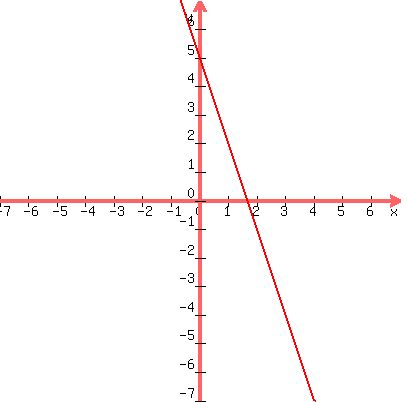Now we only have to decide whether we are to shade the
right side of the line or the left side of it. To do
this we pick any point which IS NOT on the line. Say we
choose as a test point the point (2,3) marked below with
an o, which is on the right side of the line.
Now we substitute
(x,y) = (2,3) into the inequality
3x + y < 5
If we get a true inequality, then we will shade the
same side of the line that the test point is on. If
we get a false inequality, we shade the other side:
3x + y < 5
3(2) + (3) < 5
6 + 3 < 5
9 < 5
This is false, so we shade the side OPPOSITE the
side of the line the test point that we picked is on,
namely the left side. I can't shade on here but you can on
your paper:
A shortcut would have been to have chosen the origin
(0,0) as the test point. You could have. Then you
could have substituted it in your head to decide
which side of the line to shade. Substituting
(x,y) = (0,0) you would have gotten simply
3x + y < 5
3(0) + (0) < 5
0 + 0 < 5
0 < 5
which is TRUE and which you could have done in your
head! Since it is TRUE, you would have known to
shade the side of the line which the origin (0,0)
is on. Notice that the origin (0,0) is on the left side
of the line, and that is exactly the same side we
determined that we should shade by using the test point
(2,3).
So why didn't I choose the origin (0,0) as a test point?
I would have normally, if I weren't teaching you. But
if I had you might have gotten the wrong idea that you can
ALWAYS choose the origin as a test point. But you cannot
choose the origin as a test point when the line passes
through the origin. However that is the only
time you cannot choose the origin (0,0) as a test point.
So feel free to use the origin as a test point except
when the line goes through the origin.
Edwin
