Question 845205: The area of a rectangle is 14m ^2(squared) , and the length of the rectangle is 3m less than double the width. Find the dimensions of the rectangle.
Answer by pmesler(52)   (Show Source): (Show Source):
You can put this solution on YOUR website!
So we know that the area of the rectangle is 14m^2. We also know that the length L = 2w-3 or 3m less than double the width. Whenever you see "double" that means multiply by 2.
The area of a rectangle is
A = L * W
Let's plug in the values that we know.
14 = (2w-3) * w
Combine like terms and use the distributive property.
14 = 2w^2 - 3w.
Now we have a quadratic equation, but to solve for the root of the equation, w, we need to make the left side of the equation zero. We do that by subtracting 14 from both sides to get
0 = 2w^2-3w - 14
Now, we use the quadratic formula to solve for w.
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=121 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 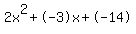 can be factored: can be factored:

Again, the answer is: 3.5, -2.
Here's your graph:
 |
Therefore the roots are (-2,0) (3.5, 0).
We can discard the negative root since you can't have a negative width. Therefore the width w = 3.5 and the length l = 2(3.5) - 3 = 4.
This checks out since A = 14m^2 and 3.5 * 4 = 14.
|
|
|