SOLUTION: Describe the vertical asymptote(s) and hole(s) for the graph of y=(x+2)(x+4)/(x+4)(x+1).

Algebra ->  Rational-functions -> SOLUTION: Describe the vertical asymptote(s) and hole(s) for the graph of y=(x+2)(x+4)/(x+4)(x+1).      Log On


   

Question 844729: Describe the vertical asymptote(s) and hole(s) for the graph of y=(x+2)(x+4)/(x+4)(x+1).
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
For x=-4 , y=%28x%2B2%29%28x%2B4%29%2F%28%28x%2B4%29%28x%2B1%29%29 does not exist, because the denominator is zero.
However, for any x%3C%3E-4 ,
y=%28x%2B2%29%28x%2B4%29%2F%28%28x%2B4%29%28x%2B1%29%29=%28x%2B2%29%2F%28x%2B1%29 which is continuous at x=-4 .
So, at x=-4 we have a hole in the graph.
The function y=%28x%2B2%29%2F%28x%2B1%29 is what results from "plugging" that hole.
For x=-1 , y=%28x%2B2%29%28x%2B4%29%2F%28%28x%2B4%29%28x%2B1%29%29 does not exist, and there is no equivalent continuous function. (No plugging possible).
At x=-1, the functions y=%28x%2B2%29%28x%2B4%29%2F%28%28x%2B4%29%28x%2B1%29%29 and y=%28x%2B2%29%2F%28x%2B1%29 have a vertical asymptote.
The function changes sign at that point.
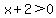y=%28x%2B2%29%2F%28x%2B1%29 is positive for x%3E-1 , where x%2B1%3E0 and x%2B2%3E0 .
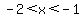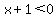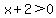It is negative for -2%3Cx%3C-1 , where x%2B1%3C0 and x%2B2%3E0 .
graph%28300%2C300%2C-6%2C4%2C-10%2C10%2C%28x%2B2%29%2F%28x%2B1%29%2C200%28x%2B1%29%29