Question 844186: A cannon ball is fired almost vertically upwards from ground level. The cannon ball has height given by the relationship H = 12t – t2 metres, where t is the time in seconds after firing.
Consider the following:
(i) If we sketch a graph of the height H against the time t after firing what shape will result?
• Draw an accurate sketch of this graph and label the graph in the context of this scenario.
(ii) How long would it take for the cannonball to reach its maximum height?
• What would be the maximum height reached?
• Re-write the relationship H in a different form using the values you obtained for the maximum height?
(iii) The maximum height reached by the cannonball is doubled. Given that the cannonball will still land after the same flight time write down a relationship for H, which would represent a doubling of the height.
(iv) Investigate further variations in the height reached. Place this data in a table and reflect on your results.
(v) Investigate what would happen if the original height is maintained but the flight time is varied.
I need help understanding the math side of this, thanks for your help
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A cannon ball is fired almost vertically upwards from ground level.
The cannon ball has height given by the relationship H = 12t – t^2 metres, where t is the time in seconds after firing.
Consider the following:
(i) If we sketch a graph of the height H against the time t after firing what shape will result?
• Draw an accurate sketch of this graph and label the graph in the context of this scenario.
I suggest you plot these points, replace x, find y
x | y
-------
0 | 0
2 | 20
4 | 32
6 | 36
8 | 32
9 | 27
12 | 0 (ground level)
Look something like this

:
(ii) How long would it take for the cannonball to reach its maximum height?
• What would be the maximum height reached?
You can see it reaches max height when t = 6 sec (halfway between 0 and 12
• Re-write the relationship H in a different form using the values you obtained for the maximum height?
In the equation h = 12t - t^2, replace t with 6
h = 12(6) - 6^2
h = 72 - 36
h = 36m (as is shown on the graph)
:
(iii) The maximum height reached by the cannonball is doubled.
Given that the cannonball will still land after the same flight time,
write down a relationship for H, which would represent a doubling of the height.
Using the form y = ax^2 + bx + c, we have to find new values for a & b, (no c)
For the coordinates:
x = 6, y = 72 (twice the height)
and
x = 12, y = 0 (same flight time)
write an equation for each pair replace x and y
36a + 6b = 72
and
144a + 12b = 0
multiply the 1st equation by 2, subtract from the 2nd equation
144a + 12b = 0
72a + 12b = 144
-----------------subtraction eliminates b, find a
72a = -144
a = -144/72
a = -2
Find b using the 1st original equation
36(-2) + 6b = 72
-72 + 6b = 72
6b = 72 + 72
6b = 144
b = 144/6
b = 24
Graph the new equation h = 24t - 2t^2
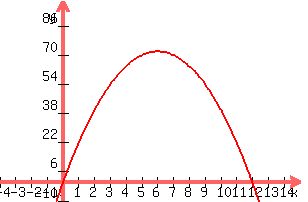
NOte that it reaches 72m in 6 sec now
:
(iv) Investigate further variations in the height reached. Place this data in a table and reflect on your results.
Note that if you want to double the height and retain the same time
double the coefficients of t and t^2, for example to double the height again to
144m
48t - 4t^2

You can make the table here using this example
:
(v) Investigate what would happen if the original height is maintained but the flight time is varied.
Using the form ax^2 + bx = y, find the a and b of the new equation
x=10, y=36; max occurs in 10 sec, but is still 36
x=20, y=0; hits the ground in 20 sec
100a + 10b = 36
400a + 20b = 0
Mult the 1st equation by 2, subtract from the 2nd
400a + 20b = 0
200a + 20b = 72
----------------subtraction eliminates b, find a
200a = -72
a = -72/200
a = -.36
Find b using the 1st original equation
100(-.36) + 10b = 36
-36 + 10b = 36
10b = 72
b = 7.2
the new equation: h = 7.2t - .36t^2, this graph looks like

max occurs at 10 sec but is still 36 m
|
|
|