Since it's a circular arrangement, we do not count the different
7 possible rotations as different arrangements, so there are 6!
ways to place the 7 girls.
Now we must place boys between each pair of girls. There are 7
spaces between the girls into which we must insert 7 "things".
These 7 "things" are either single boys or groups of boys.
These 7 "things" can either be
1. BB, BB, BB, B, B, B, B
That's 3 pairs of boys and 4 single boys.
We can choose the first pair any of 10*9 ways, the second pair
any of 8*7 ways and the third pair 6*5 ways. But, there are
3! ways we could choose which is the 1st pair, the 2nd pair and
the 3rd pair, so we must divide by 3! to avoid counting the same
group of pairs more than once. So that's 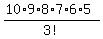 ways to make the "7 things", or
2. BBB, BB, B, B, B, B, B
That's 1 trio of boys, 1 pair of boys and 5 single boys. We can
choose the trio and of 10*9*8 ways and the pair any of 7*6 ways.
So that's 10*9*8*7*6 ways to make the 7 things
3. BBBB, B, B, B, B, B, B
That's 4 boys together and 6 single boys
There are 10*9*8*7 ways to choose the 4 that sit together.
Each of those 3 groups of 7 "things" can be inserted in those 7 spaces
in 7! ways.
My answer = 6!ū[
ways to make the "7 things", or
2. BBB, BB, B, B, B, B, B
That's 1 trio of boys, 1 pair of boys and 5 single boys. We can
choose the trio and of 10*9*8 ways and the pair any of 7*6 ways.
So that's 10*9*8*7*6 ways to make the 7 things
3. BBBB, B, B, B, B, B, B
That's 4 boys together and 6 single boys
There are 10*9*8*7 ways to choose the 4 that sit together.
Each of those 3 groups of 7 "things" can be inserted in those 7 spaces
in 7! ways.
My answer = 6!ū[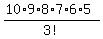 +10ū9ū8ū7ū6+10ū9ū8ū7]ū7! = 2.19469824ū1011
Edwin
+10ū9ū8ū7ū6+10ū9ū8ū7]ū7! = 2.19469824ū1011
Edwin