SOLUTION: How many different words can be formed using all the letters of the word MISSISSIPPI? In how many of these permutations do the four ‘I’s not come together? What do I do?

Algebra ->  Permutations -> SOLUTION: How many different words can be formed using all the letters of the word MISSISSIPPI? In how many of these permutations do the four ‘I’s not come together? What do I do?      Log On


   

Question 842956: How many different words can be formed using all the letters of the word MISSISSIPPI? In how many of these permutations do the four ‘I’s not come together?
What do I do?
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
How many different words can be formed using all the letters of the word MISSISSIPPI?
If they were all distinguishable, the answer would be 11!.
But since the 4 I's are indistinguishable we must divide by 4!,
and since the 4 S's are indistinguishable we must also divide by 4! again,
and since the 2 P's are indistinguishable we must also divide by 2!

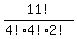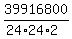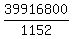Answer: 11%21%2F%284%214%212%21%29 = 39916800%2F%2824%2A24%2A2%29 = 39916800%2F1152 = 34650
In how many of these permutations do the four 'I's not come together?
We must subtract all the ways the I's come together.

That's the distinguishable arrangements of these 8 "things"

(IIII),M,S,S,S,S,P,P

If they were all distinguishable, the answer would be 8!.
But since the 4 S's are indistinguishable we must divide by 4!,
and since the 2 P's are indistinguishable we must also divide by 2!

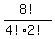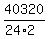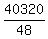So we must subtract 8%21%2F%284%212%21%29 = 40320%2F%2824%2A2%29 = 40320%2F48 = 840

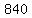So we subtract the 840 ways the I's come together from the 34650 and
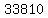get 33810 

Edwin