Question 84178: Find the GCF of 90m2np3 and 150mn3p2.
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! The Greatest Common Factor (GCF) is the largest possible number/variable expression that divides evenly into both of the given quantities.
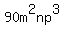 and and 
The numbers that divide evenly into BOTH 90 and 150 would be
1, 2, 3, 5, 6, 10, 15, and 30. The largest such number is 30.
You also have common factors of m, n, and p. Since m divides evenly into m^2 but NOT viceversa, m is a common factor. Actually, it turns out that when variables raised to different powers are involved, you can just choose the LOWEST POWER each factor. By this way of thinking, you can determine that n is a common factor (when compared to n^3), and also p^2 is a common factor (when compared to p^3).
Therefore, putting it all together, the GCF =  . .
R^2 at SCC
|
|
|