SOLUTION: "Use the product formula (A+B)(A-B)= (A^2-B^2) to evaluate these products in your head. 49 * 51, 998 * 1002." Not a clue on how to do this.

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: "Use the product formula (A+B)(A-B)= (A^2-B^2) to evaluate these products in your head. 49 * 51, 998 * 1002." Not a clue on how to do this.      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 841761: "Use the product formula (A+B)(A-B)= (A^2-B^2) to evaluate these products in your head. 49 * 51, 998 * 1002."
Not a clue on how to do this.
Answer by josgarithmetic(39628) About Me  (Show Source):
You can put this solution on YOUR website!
The big clue is each product is of a form, (a+b)(a-b). This allows you to take advantage of the difference of squares.

Let me create an example, different from the ones you ask for.

Find 201*205.
Write each factor as a form, (a-b)(a+b).
What number is in the exact middle of 201 and 205? %28201%2B205%29%2F2=406%2F2=203.
Use 203 and add something to get 200+w and subtract the same something to get 200-w. You are creating the expression, using in this case, w=2, to become (203-w)(203+w), specifically 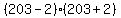%28203-2%29%28203%2B2%29.

You see that you have, according to the difference of squares formula,
highlight_green%28201%2A205=%28203-2%29%28203%2B2%29=203%5E2-2%5E2%29, which you should be able to compute fast.