SOLUTION: Find a, b, and c for the function f(x) = a sin(bx − c) such that the graph of f matches the figure. http://www.sendspace.com/file/zfod3n

The basic graph of y = sin(x) has these 5 major points, 

zero,max,zero,min,zero, which are:

(0,0), (,1), ,0), (,1), (,0)

Your graph has the corresponding 5 major points, starting
with the point nearest the origin:

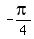(,0), (,-3), ,0), (,1), (,0)

The period is  since the last x value of the five is , and
the first of the five is 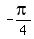, so they have difference 

===, 

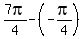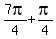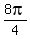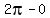same as the basic sine graph, = so there is no horizontal
stretching or shrinking.

Each of the 5 major x-coordinates of your graph is pi/4 less than its
corresponding x-coordinate on the basic sine graph:

=====

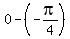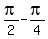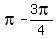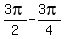So the horizontal shift, commonly called the phase shift, is  units to the 
left.  Therefore the equation of your graph will have (x-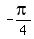) or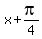 substituted
for x.

Each of the 5 major y-coordinates of the basic sine graph are 0,1,0,-1,0,
whereas the 5 corresponding major y-coordinates of your graph are 0,-3,0,3,0,
They are all multiplied by -3.  The negative sign reflects the graph in the 
x-axis and the 3 stretches it by a factor of 3 vertically.  Therefore the right
side of the equation of your graph will have a factor of -3.  So the equation
of your graph is found by starting with the basic sine graph:

y = sin(x)

Then replace the x by 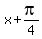 and multiply the right side by -3, and get

y = -3sin.

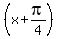Edwin