You start your question with "hence", so we cannot be sure
what went before that, and how you are supposed to come up
with x and y. I observe that the three numbers given 3,10,21
appear in Pascal's triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
Pascal's triangle is composed of binomial coefficients which
are combinations:
3 = C(3,2), 10 = C(5,2), 21 = C(7,2)
So I assume that the sequence 3,x,10,y,21 is this sequence:
3=C(3,2), x=C(4,2), 10=C(5,2), y=C(6,2), 21=C(7,2)
 ,
, ,
, ,
, ,
, So the nth term is
So the nth term is  , and they are called
"triangular" numbers, because they are the numbers of dots
that can be formed into a triangular arraylike this: .
. . .
. . . . . .
. . . . . . . . . .
. . . . . . . . . . . . . . .
3 = . . 6 = . . ., 10 = . . . ., 15 = . . . . ., 21 = . . . . . .
We need to prove that the sum of any two consecutive terms of this sequence
3,6,10,15,21,... is a perfect square. We can see that 3+6=9=3², 6+10=16=4²,
10+15=25=5², 15+21=36=6². We need to prove this in general:
Proof:
the nth term is
, and they are called
"triangular" numbers, because they are the numbers of dots
that can be formed into a triangular arraylike this: .
. . .
. . . . . .
. . . . . . . . . .
. . . . . . . . . . . . . . .
3 = . . 6 = . . ., 10 = . . . ., 15 = . . . . ., 21 = . . . . . .
We need to prove that the sum of any two consecutive terms of this sequence
3,6,10,15,21,... is a perfect square. We can see that 3+6=9=3², 6+10=16=4²,
10+15=25=5², 15+21=36=6². We need to prove this in general:
Proof:
the nth term is 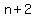 and
the (n+1)st term is
and
the (n+1)st term is  =
=  Add them:
Add them:
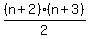



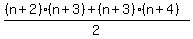

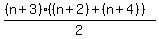

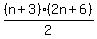

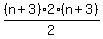

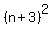 which is a perfect square.
Edwin
which is a perfect square.
Edwin