What is the vertex form of y=(3x+1)(x-2)
Foil it out
y = 3x² - 6x + x - 2
y = 3x² - 5x - 2
Factor the coefficient of x², which is 3,
out of the first two terms only: Not to
take 3 out of -5x you divide -5 by 3 and get
 y = 3(x² -
y = 3(x² -  x) - 2
Take one-half the coefficient of x:
x) - 2
Take one-half the coefficient of x:
 ·
· =
=  Then square what you get:
Then square what you get:
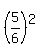 =
= 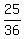 Add that and then subtract it inside the parentheses:
y = 3(x² -
Add that and then subtract it inside the parentheses:
y = 3(x² -  x +
x + 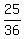 -
- 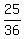 ) - 2
Change the parentheses to brackets so we can factor
and put parentheses inside:
y = 3[x² -
) - 2
Change the parentheses to brackets so we can factor
and put parentheses inside:
y = 3[x² -  x +
x + 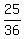 -
- 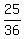 ] - 2
Factor the first three terms inside the brackets:
y = 3[(x -
] - 2
Factor the first three terms inside the brackets:
y = 3[(x -  )(x -
)(x -  ) -
) - 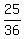 ] - 2
Write (x -
] - 2
Write (x -  )(x -
)(x -  ) as (x -
) as (x -  )²
y = 3[(x -
)²
y = 3[(x -  )² -
)² - 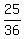 ] - 2
Now remove the brackets by distributing the 3 into the
bracket, leaving the (x -
] - 2
Now remove the brackets by distributing the 3 into the
bracket, leaving the (x -  )² intact.
y = 3(x -
)² intact.
y = 3(x -  )² - 3·
)² - 3·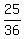 - 2
Simplify the last two terms:
y = 3(x -
- 2
Simplify the last two terms:
y = 3(x -  )² -
)² - 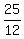 - 2
y = 3(x -
- 2
y = 3(x -  )² -
)² - 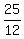 -
- 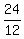 y = 3(x -
y = 3(x -  )² -
)² - 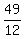 Compare that to:
y = a(x - h)² + k
and equate like parts of the two equations:
a = 3,
-h =
Compare that to:
y = a(x - h)² + k
and equate like parts of the two equations:
a = 3,
-h = 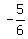 , so h =
, so h =  k =
k = 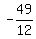 So the vertex is the point (
So the vertex is the point ( ,
, 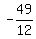 ), or
like (.8, 4.1)
or a mixed fraction is better for graphing:
The vertex is the point (
), or
like (.8, 4.1)
or a mixed fraction is better for graphing:
The vertex is the point ( , -(4
, -(4 )
Nasty fractions, indeed, but nasty fractions don't bother
computers, so why should they bother us humans? :-)
But if we can get some more points we can plot the graph.
The graph will be a parabola and we can observe if that
point really and truly is the vertex:
We can get the y-intercept by going back to the original
equation y=(3x+1)(x-2) and substituting x=0. We get
y = (3·0+1)(0-2) = (0+1)(-2) = (1)(-2) = -2
So we plot those two points and a bunch of others, we get
this graph.
)
Nasty fractions, indeed, but nasty fractions don't bother
computers, so why should they bother us humans? :-)
But if we can get some more points we can plot the graph.
The graph will be a parabola and we can observe if that
point really and truly is the vertex:
We can get the y-intercept by going back to the original
equation y=(3x+1)(x-2) and substituting x=0. We get
y = (3·0+1)(0-2) = (0+1)(-2) = (1)(-2) = -2
So we plot those two points and a bunch of others, we get
this graph.
 Edwin
Edwin