Question 840297: I really need some help! Can anyone help me?
If f(x)=ln x, g(x)=e^4^x, and h(x)= x^3, find the following
a. (f*g)(x)
what is the domain of f*g?
b. (g*f)(x)
what is the domain of g*f?
c. (f*h)(x)
what is the domain of f*h?
Answer by sheldonbbtrocks(115)   (Show Source): (Show Source):
You can put this solution on YOUR website! Okay, we first need to find the composition of functions. For the first one you take the function of g(x) and plug it into wherever there is an x in f(x).
When we do this (f*g)(x) becomes y=ln(e^4^x)
Remember, the domain is all of the x-values on a graph. Here is the graph:
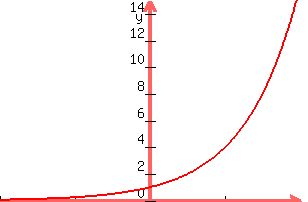
As you can tell, the graph will go on in the x and y directions, so the domain is all reall numbers (-infinity,infinity)
Now we will compute (g*f)(x) Using the same method as above; we get y=e^4^(lnx)
Sadly, this program won't let me graph the function, however, if you do it on a calculator or WolframAlpha you will see that the x values will go from negative to positive infinity, again, making the domain all real numbers
(-infinity,infinity)
Now for (f*h)(x) we will do the same thing as before; we get y=ln(x^3)
Let's graph it: 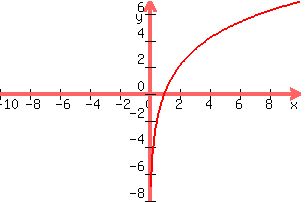
Now we see something different, there are no negative x values. This means that the domain is all positive real numbers or (0,infinity).
I hope this helped you!
|
|
|