|
Question 840292: I really need some help! Can anyone help me?
Use the given zero to find the remaining zeros of the function
h(x)=3x^4+7x^3+69x^2+175x-150; zero:-5i
Found 2 solutions by Alan3354, josh_jordan:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Use the given zero to find the remaining zeros of the function
h(x)=3x^4+7x^3+69x^2+175x-150; zero:-5i
-------------
Complex zeroes occur in pairs, so +5i is a zero.
--> (x^2 + 5) is a factor
Divide by x^2+5
Answer by josh_jordan(263)   (Show Source): (Show Source):
You can put this solution on YOUR website! We know that if -5i is a zero of the polynomial, then 5i must also be a zero. If we rewrite these two zeros in factor form, we would have
(x + 5i)(x - 5i)
Now, let's expand that, by using the FOIL method. This will give us:
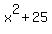
Now, we have a factor of our original polynomial without the i's. Now, we can use polynomial long division to divide our original function by 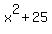 . Doing this will give us: . Doing this will give us:
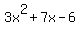
Now, we can factor this polynomial. This will give us, in factored form:
(3x - 2)(x + 3)
Setting each of these factors equal to zero, will give us our our other two zeroes:
3x - 2 = 0 -------> 3x = 2 -----> x = 2/3
and
x + 3 = 0 -----> x = -3
Since the highest degree of our original polynomial function is 4, and we now have found 4 zeroes, we are done.
Zereos: -5i, 5i, 2/3, -3
|
|
|
| |