Question 839898: The Gare Montparnasse train station in Paris has a high-speed version of a moving walkway. If he walks while riding this moving walkway, Jean Claude can travel 200 meters in 30 seconds less time than if he stands still on the moving walkway. If Jean Claude walks at a normal rate of 1.5 meters per second, what is the speed of the Gare Montparnasse walkway?
Found 3 solutions by richwmiller, ikleyn, josgarithmetic:
Answer by richwmiller(17219)   (Show Source): (Show Source):
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The Gare Montparnasse train station in Paris has a high-speed version of a moving walkway.
If he walks while riding this moving walkway, Jean Claude can travel 200 meters in 30 seconds
less time than if he stands still on the moving walkway. If Jean Claude walks at a normal rate
of 1.5 meters per second, what is the speed of the Gare Montparnasse walkway?
~~~~~~~~~~~~~~~~~~~
Let x be the speed of the walkway, in meters per second.
When Jean Claude stands still on the walkway, he actually moves relatively to the floor
at the speed of x m/second.
The time to travel 200 meters at this speed is  seconds.
When Jean Claude walks on the walkway with his relative speed of 1.5 m/s relative to the walkway,
he actually moves relatively to the floor at the speed of (1.5+x) m/second.
The time to travel 200 meters at this speed is seconds.
When Jean Claude walks on the walkway with his relative speed of 1.5 m/s relative to the walkway,
he actually moves relatively to the floor at the speed of (1.5+x) m/second.
The time to travel 200 meters at this speed is 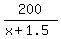 seconds.
The difference of the two travel times is 30 seconds - so, we write this time equation seconds.
The difference of the two travel times is 30 seconds - so, we write this time equation
 - - 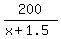 = 30 seconds. (1)
This is your setup equation.
At this point, the setup is complete, and now your task is to solve it.
To solve the equation, multiply both sides by x*(x+1.5). You will get
200*(x+1.5) - 200*x = 30x*(x+1.5).
Simplify step by step
200x + 300 - 200x = 30x^2 + 45x,
300 = 30x^2 + 45x,
divide all the terms by 15
20 = 2x^2 + 3x,
2x^2 + 3x - 20 = 0.
Apply the quadratic formula = 30 seconds. (1)
This is your setup equation.
At this point, the setup is complete, and now your task is to solve it.
To solve the equation, multiply both sides by x*(x+1.5). You will get
200*(x+1.5) - 200*x = 30x*(x+1.5).
Simplify step by step
200x + 300 - 200x = 30x^2 + 45x,
300 = 30x^2 + 45x,
divide all the terms by 15
20 = 2x^2 + 3x,
2x^2 + 3x - 20 = 0.
Apply the quadratic formula
 = = 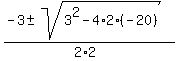 = = 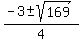 = = 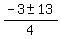 .
You want the positive root x = .
You want the positive root x =  = =  = 2.5 m/s.
It is the speed of the walkway. ANSWER
CHECK. Check the validity of equation (1): = 2.5 m/s.
It is the speed of the walkway. ANSWER
CHECK. Check the validity of equation (1): 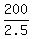 - - 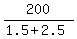 = = 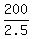 - - 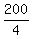 = 30.0 seconds.
Which is precisely correct ! = 30.0 seconds.
Which is precisely correct !
At this point, the problem is solved completely.
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
|
|
|