SOLUTION: Find three consecutive positive odd integers such that the product of the first and third is equal to one less then twice the second (only an algebraic solution wjll be excepted)

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: Find three consecutive positive odd integers such that the product of the first and third is equal to one less then twice the second (only an algebraic solution wjll be excepted)       Log On


   

Question 839258: Find three consecutive positive odd integers such that the product of the first and third is equal to one less then twice the second (only an algebraic solution wjll be excepted)
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,

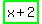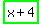
three consecutive positive odd integers:highlight_green%28x%29,highlight_green%28x%2B2%29,highlight_green%28x%2B4%29

Question states***product of the first and third is equal to one less then twice the second

***  x(x+4) = 2(x+2) - 1

    x^2 + 2x -3 = 0

   (x + 3)(x - 1) = 0,   x  = 1 (positive odd integers)

The three consecutive positive odd integers are:  1, 3,  5

CHECKING our answer***

 1%2A5+=+2%2A3+-+1+=+5

Wish You the Best in your Studies.