Question 838283: My name is Robert Brown and the question is:
"Without solving, determine the character of the solutions of each equation in the complex number system. Verify your answer using a graphing utility."
73) 3x^2 - 3x +4=0
I have a test TODAY and no one at the school is willing to help me
Found 2 solutions by richard1234, KMST:
Answer by richard1234(7193)   (Show Source):
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! SOLUTION (or verification) BY GRAPHING:
That is a quadratic equation.
The left hand side, 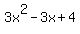 is a polynomial of degree 2 (a quadratic polynomial).
The function  is a quadratic function.
Quadratic functions graph as parabolas.
If you graph ,
you can see where the graph crosses or touches the x-axis (if it ever does).
That could happen at 2, 1, or zero points.
At those points, if any,  .
The x-coordinates of those points are the real solutions of  .
Since all real numbers are also complex numbers, those can be called complex solutions, but there is no imaginary part to them.
Every quadratic equation has "two complex number solutions",
but there is a trick (coming) about that "two".
If the graph touches the axis at just one point, as in the graph below, the solution is a double real solution. It counts as "two" real solutions, and there are no solutions with anything imaginary about them.
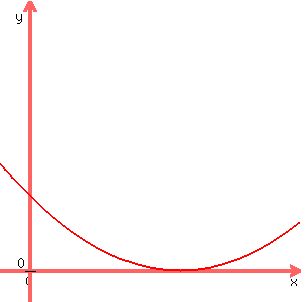
If the graph of does not touch or cross the x-axis at all,
has two complex solutions of the form  ,
with a non-zero imaginary part.  .
SOLVING WITH SOME CALCULATIONS:
Quadratic equations can be written in the form 
where  ,  , and  are numbers called coefficients.
The solutions are given by
With some calculation you know if all the solutions are real.
You do not need to calculate the values of the solutions.
If 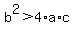 <-->  , the square root is a non-zero real number,
and you have two different real solutions.
If  <-->  , the square root is zero,
and you have one (double) real solution.
If  <-->  ,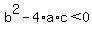
the square root is a purely imaginary number,
 ,
and you know that there are
two conjugate complex solutions that can be written (both together) as
 .
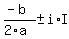In your case,  ,  , and 
and you have no real solutions.
We so not need to calculate
 , or
 , or
 , or
 , or the solutions
 , or
|
|
|
