|
Question 838243: Tom and Tyanna are training at the track. Tom can complete a lap in 40 seconds. Tyanna and Tom begin at the same start/finish line and at the same time but run in opposite directions. Although different, their individual speeds remain constant and they pass each other every 15 seconds.
Completing her workout, Tyanna stops after finishing 12 laps. Tom continues to run at the same rate.
Your tasks are to determine:
a) How many times Tyanna and Tom passed each other (going in opposite directions) during the time they were both running
b) How many more minutes and seconds and exactly how many more laps Tom will need to run to have run exactly the same distance that Tyanna ran.
Requirement: You will need to present some appropriate time/distance/lap tables and/or diagrams to assist the reader in understanding your solution, especially your explanation of that solution
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The requirement refers to a table that is the way the teacher would solve the problem. Not being in your class, I do not know the teacher's way to solve it.
MY WAY:
Tom runs 1 lap in  seconds, so Tom's speed, in laps per second, is seconds, so Tom's speed, in laps per second, is  . .
Tom and Tyanna together cover 1 lap in  seconds, so their speeds add up to seconds, so their speeds add up to  laps per second. laps per second.
Tyanna's speed, in laps per second, is
 . .
That means that Tyanna runs 1 lap in  seconds. seconds.
It took  for Tyanna to run her 12 laps. for Tyanna to run her 12 laps.
During that time Tyanna and Tom passed each other  because because

They passes each other for the 19th time
 after they started running, and 3 seconds later Tyanna was finished. after they started running, and 3 seconds later Tyanna was finished.
To ruAt  seconds per lap, it would take Tom a total of seconds per lap, it would take Tom a total of
 to run 12 laps, the same distance that Tyanna ran. to run 12 laps, the same distance that Tyanna ran.
Since Tyanna finished in  , Tom will need to run , Tom will need to run
 more after Tyanna is finished. more after Tyanna is finished.
That is  , because dividing , because dividing 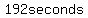 by by  seconds per minute gives you a quotient of 3 minutes and a remainder of 12 seconds. seconds per minute gives you a quotient of 3 minutes and a remainder of 12 seconds.
During those extra 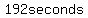 , at a speed of , at a speed of  laps per second Tom will cover laps per second Tom will cover
 = =
|
|
|
| |