SOLUTION: Logbase3(logbase2(x))+logbase1/3(logbase1\2(y))=1 x(y^2)=4

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Logbase3(logbase2(x))+logbase1/3(logbase1\2(y))=1 x(y^2)=4      Log On


   

Question 838117: Logbase3(logbase2(x))+logbase1/3(logbase1\2(y))=1
x(y^2)=4
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
First of all, please include the instructions for the problems you post. Tutors are less like to respond if the problem is not clear.

I'm guessing that the instructions are to solve this system of equations.
log%283%2C+%28log%282%2C%28x%29%29%29%29%2Blog%281%2F3%2C%28log%281%2F2%2C%28y%29%29%29%29=1
x%28y%5E2%29=4

We will be using the Substitution Method. We will solve the second equation for x and then substitute what we get into the first equation. But before we do that we will transform the first equation into a simpler, more useable form.

Among other things we will combine the logs. The logs we have are not like terms so we cannot just add them. (Like logarithmic terms have the same bases and the same arguments.) But we could use a property of logs, log%28a%2C+%28p%29%29+%2B+log%28a%2C+%28q%29%29+=+log%28a%2C+%28p%2Aq%29%29 or log%28a%2C+%28p%29%29+-+log%28a%2C+%28q%29%29+=+log%28a%2C+%28p%2Fq%29%29, to combine them if we can get the bases equal. So we will start by using the change of base formula, log%28a%2C+%28p%29%29+=+log%28b%2C+%28p%29%29%2Flog%28b%2C+%28a%29%29, to change the base 1/3 log into an expression of base 3 logs:

Fortunately we know the log in the denominator. The power of 3 that result in 1/3 is -1. So now we have:

or
log%283%2C+%28log%282%2C%28x%29%29%29%29-log%283%2C%28log%281%2F2%2C%28y%29%29%29%29=1

Now we can use log%28a%2C+%28p%29%29+-+log%28a%2C+%28q%29%29+=+log%28a%2C+%28p%2Fq%29%29 to combine the two logs:
log%283%2C+%28log%282%2C%28x%29%29%2Flog%281%2F2%2C%28y%29%29%29%29=1
This will simplify if we change the base 1/2 log into an expression of base 2 logs (using the base conversion formula again):

Again we know the last denominator:
log%283%2C+%28log%282%2C%28x%29%29%2F%28log%282%2C%28y%29%29%2F%28-1%29%29%29%29=1
or
log%283%2C+%28log%282%2C%28x%29%29%2F%28-log%282%2C%28y%29%29%29%29%29=1
or
log%283%2C+%28-log%282%2C%28x%29%29%2Flog%282%2C%28y%29%29%29%29=1

We can "peel off" the outer log if we rewrite this in exponential form. In general, log%28a%2C+%28p%29%29+=+n is equivalent to p+=+a%5En Using this pattern on our equation we get:
-log%282%2C%28x%29%29%2Flog%282%2C%28y%29%29=3%5E1
or
-log%282%2C%28x%29%29%2Flog%282%2C%28y%29%29=3
Multiplying both sides by -1:
log%282%2C%28x%29%29%2Flog%282%2C%28y%29%29=-3

We could now start with the substitution from the other equation. But we might recognize that the fraction there matches the pattern of the right side of the base conversion formula. The fraction is what we would get if we converted 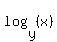log%28y%2C+%28x%29%29 into base 2 logs. So we can simplify this even more:
log%28y%2C%28x%29%29=-3
(If this step is too confusing, then just go back and use the previous equation.

We're finally ready to start the Substitution Method. Solving x%28y%5E2%29+=+4 for x we get x+=+4%2Fy%5E2. Substituting this in for x into our simplified log equation we get:
log%28y%2C%284%2Fy%5E2%29%29=-3
Now we solve for y. Rewriting this in exponential form we get:
4%2Fy%5E2=y%5E%28-3%29
Multiplying both sides by y%5E2:
4=y%5E%28-3%29+%2A+y%5E2
or
4=y%5E%28-1%29
which means
1%2F4+=+y

Now we solve for x. Using x+=+4%2Fy%5E2:
x+=+4%2F%281%2F4%29%5E2
x+=+4%2F%281%2F16%29
x=4%2A%2816%2F1%29
x+=+64

Last we check. This is not optional when logarithmic equations are involved. We must check to make sure all bases and all arguments of all logs remain valid for the solution(s). (Valid arguments are positive but not 1's and valid arguments are positive.) Use the original equation to check:
log%283%2C+%28log%282%2C%28x%29%29%29%29%2Blog%281%2F3%2C%28log%281%2F2%2C%28y%29%29%29%29=1
Checking x = 64 and y =1/4:

The bases all look OK. And the base 2 and base 1/2 logs are good. But we have to find out what the base 2 and 1/2 logs are so we can determine if the base 3 and 1/3 logs are OK. Since 2%5E6=64 and %281%2F2%29%5E2+=+1%2F4 we know what the base 2 and base 1/2 logs are:
log%283%2C+%286%29%29%2Blog%281%2F3%2C%282%29%29=1
And we can now see that the base 3 and base 1/3 logs are OK, too. (If at any point in the check any base or any argument of any logs had been invalid, then we would have to reject our solution (which would mean that the system had no solution).

So our solution of (64, 1/4) is correct.