SOLUTION: Steven absurd some red dye to turn himself red for Valentine's day. If the half-life of the dye is 2 hours, and there is only 20mg of dye left in him after 15 hours, what is the or

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Steven absurd some red dye to turn himself red for Valentine's day. If the half-life of the dye is 2 hours, and there is only 20mg of dye left in him after 15 hours, what is the or      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 837970: Steven absurd some red dye to turn himself red for Valentine's day. If the half-life of the dye is 2 hours, and there is only 20mg of dye left in him after 15 hours, what is the original amount of the dye he took?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
y= amount of dye left in Steven, in mg, at time t in hours.
A= original amount of the dye, in mg, that he took, and had inside at t=0 .

THE (precocious) FIFTH GRADER THOUGHTS:
Since the half-life of the dye is 2 hours,
after 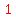red%281%29 half-life, at t%2F2=red%281%29 , and
y=A%2A%281%2F2%29 is half of the original amount
After red%282%29 half-lives, t%2F2=red%282%29 another half-life has passed, and
y=%28A%2A%281%2F2%29%29%2A%281%2F2%29=A%2A%281%2F2%29%5Ered%282%29 .
Another half-life after that, after red%283%29 half-lives, t%2F2=red%283%29 , and
y=%28A%2A%281%2F2%29%5E2%29%2A%281%2F2%29=A%2A%281%2F2%29%5Ered%283%29 .
The pattern tells me that at 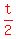red%28t%2F2%29half-lives the amount left is
y=A%2A%281%2F2%29%5Ered%28t%2F2%29=A%2F2%5Ered%28%22t+%2F+2%22%29 .
So if 20=A%2F2%5E%22t+%2F+2%22 , A=20%2A2%5E%22t+%2F+2%22 .
Since t=17 , t%2F2=17%2F2=8%261%2F2 , and 256%2A1.414 .
A good approximate solution is
A=20%2A256%2A1.414=7239.68=%22approx+.%22highlight%287240%29 .
Steven took in 7240 mg (7.24 grams) of red dye.

THE PRE-CALCULUS STUDENT THOUGHTS:
I know the teacher said this type of problem is an example of exponential decay, and there is a formula for this.
It is an exponential function, with that irrational letter e and a complicated exponent.
There was t in that exponent, and something else, maybe the half-life, or some strange constant, or both.

THE PRE-CALCULUS STUDENT WITH HELP FROM THE FIFTH GRADER:
I do mot enjoy memorizing and blindly applying formulas.
I keep forgetting those formulas, anyway.
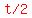y=A%2F2%5Ered%28%22t+%2F+2%22%29
That red%28%22t+%2F+2%22%29 is the number of half-lives,
because in this problem the half-life is t%5B%221%2F2%22%5D=red%282%29 ,
and so t%2Ft%5B%221%2F2%22%5D=red%28t%2F2%29 is the number of half-lives.
ln%28y%29=ln%28A%2F2%5Ered%28%22t+%2F+2%22%29%29
ln%28y%29=ln%28A%29-ln%282%5Ered%28%22t+%2F+2%22%29%29 --> ln%28y%29%2Fln%28A%29=-red%28t%2F2%29%2Aln%282%29 --> ln%28y%29-ln%28A%29=-ln%282%29%2Ared%28t%2F2%29 --> ln%28y%2FA%29=-ln%282%29%2A%28t%2Ft%5B%221%2F2%22%5D%29 --> ln%28y%2FA%29=-ln%282%29%2At%2Ft%5B%221%2F2%22%5D --> ln%28y%2FA%29=-%28ln%282%29%2Ft%5B%221%2F2%22%5D%29%2At
I think that factor was called lambda or k ,
lambda=ln%282%29%2Ft%5B%221%2F2%22%5D ,
and you can write
ln%28y%2FA%29=-lambda%2At --> y%2FA=e%5E%28-lambda%2At%29 --> y=A%2Ae%5E%28-lambda%2At%29
Oh, and we were supposed to use the approximate value ln%282%29=0.693 ,
so lambda=0.693%2F2-0.3465 for this problem, so y=A%2Ae%5E%28-0.3465%2At%29.
At t=17 , we have 20=A%2Ae%5E%28-0.3465%2A17%29
Solving for A ,
A=20%2Fe%5E%28-0.3465%2A17%29=20%2Fe%5E%28-5.8905%29=20%2F0.00276559(rounding)
So A=7232 (rounded).
What about using a better approximation for 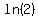ln%282%29 ?
With all the digits my calculator carries, A=7241 (rounded).