Question 837931: Let P(x)=x^3-3x^2+2 and Q(x)= x^2-6x+11
Find all values of x such that P(x)=Q(x)
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! First of all, these are not exponential functions (which have variables in the exponents). These are polynomial functions. (I have changed the category to the appropriate one.)
If P(x) = Q(x) then
Now we solve for x. To solve polynomials like this we want one side to be zero. Subtracting the entire right side from both sides we get:
And now we factor. The GCF is 1, this does not fit any of the factoring patterns and it is not a trinomial. And since I don't see how to use factoring by grouping, it appears that we must resort to trial and error of the possible rational roots.
The possible rational roots of any polynomial are all the ratios, positive and negative, which can be formed using a factor of the constant term (at the end) in the numerator and a factor of the leading coefficient (at the front) in the denominator. With a constant term of 9 (whose factors are 1, 3 and 9) and a leading coefficient of 1, our possible rational roots are:
+1/1, +3/1 and +9/1
which simplify to:
+1, +3 and +9
We can check 1 (and perhaps -1) with mental math. Neither one works here. SO we'll try 3. Synthetic division is often used when mental math is not practical:
3 | 1 -4 6 -9
---- 3 -3 9
-----------------
1 -1 3 0
And we have a root! The remainder, in the lower right corner, is zero. This means that 3 is a root (and that (x-3) is a factor) of  Not only that, the rest of the bottom row tells us the other factor. The "1 -1 3" translates into  .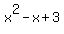
This other factor is a quadratic. It does not factor but we can use the quadratic formula:
Simplifying...
which is short for:
 or 
or (in standard a + bi form):
 or 
So there are three values of x that make P(x) = Q(x): 3,  ,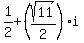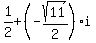 
|
|
|
