|
Question 837764: I'm a little bit confused as to what I am really doing. A few classmates had said to use the foiling method but it does not look right. The directions state: Describe how to transform the parent function y=x2 (sqaured) to the graph of each function below. Graph both functions on the same axes...
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There is a role for algebraic manipulations based on that "foiling method", or a "completing the square" method", depending on what form of the function they give you. However, I am guessing that your problem does not require that. (I have to guess because I do not know what functions or graphs you were given).
Because I am guessing what you need to know, I will cover many possibilities and the answer will be long.
When teachers talk about "transform" and "parent function" to graph a function,
you have to use either
A) your brain, or
B) "recipes" from the book or from the teacher
to change the known graph of the "parent function" into a similar graph for the function given, or to match a given graph.
From the "parent function"  you can derive many related functions. Their graphs look similar but moved ("translated" or "shifted") left or right, and/or up or down, and/or "stretched" or "shrunken" horizontally or vertically, and/or "flipped". you can derive many related functions. Their graphs look similar but moved ("translated" or "shifted") left or right, and/or up or down, and/or "stretched" or "shrunken" horizontally or vertically, and/or "flipped".
I'll give you examples, and what my brain tells me about them. They may remind you of "recipes" and "rules" you got from school and books.
When you have to "describe" or "explain", it is better to follow the teacher's (or book's) favorite wordings and recipes, because independent use of your brain may not be understood, or accepted.
The graph of  looks like this: looks like this:

SHIFTING/TRANSLATING VERTICALLY:
If you wanted the graph of  you would just move each point in that graph 3 units up, so both functions graphed on the same axes would look like this: you would just move each point in that graph 3 units up, so both functions graphed on the same axes would look like this:
 (Just for illustration, I marked 3 of the points, and drew the arrows showing how they change from one graph to the other. Your teacher most likely does not want to see the arrows, or the marked points). All the points in the graph move the same way. The whole graph moves (is "translated" or "shifted") 3 units up. (Just for illustration, I marked 3 of the points, and drew the arrows showing how they change from one graph to the other. Your teacher most likely does not want to see the arrows, or the marked points). All the points in the graph move the same way. The whole graph moves (is "translated" or "shifted") 3 units up.
Similarly, the graph of  is like the graph of is like the graph of  , but with all points moved ("translated" or "shifted") 2 units down. , but with all points moved ("translated" or "shifted") 2 units down.
SHIFTING/TRANSLATING HORIZONTALLY:
If you add a number to the  before applying the function, you have a different effect. before applying the function, you have a different effect.
The graph for  has has  for for  , ,  for for  , ,
and  for for  . .
The graph for  would have would have  for for  , where , where  . .
It would have  for for  , where , where  . .
It would have  for for  , where , where  . .
All the points would be moved 3 units to the right because you have  where you had just where you had just  : :
 (Just for illustration, I marked 3 of the points, and drew the arrows showing how they change from one graph to the other. Your teacher most likely does not want to see the arrows, or the marked points). All the points in the graph move the same way. The whole graph moves (is "translated") 3 to the right. (Just for illustration, I marked 3 of the points, and drew the arrows showing how they change from one graph to the other. Your teacher most likely does not want to see the arrows, or the marked points). All the points in the graph move the same way. The whole graph moves (is "translated") 3 to the right.
Similarly, the graph of  is like the graph of is like the graph of  , but with all points moved ("translated" or "shifted") 1 unit to the left. , but with all points moved ("translated" or "shifted") 1 unit to the left.
STRETCHING AND SHRINKING VERTICALLY:
A factor in front of the square has a different effect.
The graph of  is like the graph of is like the graph of  , but "vertically stretched", because for each , but "vertically stretched", because for each  , ,  assigns a assigns a  value twice as great as value twice as great as  : :

Something like that would happen for any other factor greater than 1.
For factors between 0 and 1, the graph would look vertically "shrunken", as shown below for  and and  . .

FLIPPING (also called "reflecting"):
A minus sign in front of the function flips  over the x-axis turning it into over the x-axis turning it into  as shown below: as shown below:

The "transformation" could be called "flipping" or "reflecting" over the x-axis.
Putting a minus sign in front of the function can be seen as multiplying the whole function times  , since , since  . .
Any negative factor, would flip and at the same time stretch or shrink the graph vertically, as shown below for  , ,  , and , and 

OTHER CHANGES:
You could talk about stretching and shrinking horizontally, and about flipping over the y-axis. That would involve applying a factor to the  before applying the function. before applying the function.
However, with  (squaring) as the "parent function", I would avoid those moves. (squaring) as the "parent function", I would avoid those moves.
COMBINATIONS:
You could do several transformations to the function in a certain order.
Sometimes the same result can be obtained in more that one way.
EXAMPLES:
Say you are given the graph below. How was  transformed to get that? transformed to get that?
 It was flipped upside down, so there is a minus sign up front. It was flipped upside down, so there is a minus sign up front.
The graph looks stretched vertically, so there is a factor up front with an absolute value greater than 1.
The vertex has been moved from (0,0) 4 units to the left, and 8 units up to (-4,8).
A shift 4 units to the left means that what was squared is 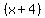 . .
A shift up by 8 units means there is a 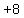 at the end. at the end.
What about the vertical stretch?
For  , points where , points where  is 1 unit away from the vertex at (0,0) have is 1 unit away from the vertex at (0,0) have
 , 1 unit away from the , 1 unit away from the  at the vertex. at the vertex.
This function, for  1 unit away from the vertex we are at 1 unit away from the vertex we are at  or at or at  . At those points we seem to have . At those points we seem to have  , so we are , so we are  units away from the units away from the  at the vertex, so at the vertex, so  (with the minus sign for the flip) is my factor, and I can write the function as (with the minus sign for the flip) is my factor, and I can write the function as

I would say that from  the function has been the function has been
flipped (or reflected) over the x-axis,
vertically stretched by a factor of 12,
shifted (or moved, or translated) 4 units left, and
shifted (or moved, or translated) 8 units up.
Say you are given the function  . .
The transformations from  are listed below, followed by the graphs. are listed below, followed by the graphs.
The  that is squared means a 1 unit shift to the left. that is squared means a 1 unit shift to the left.
The  at front means a vertical stretch by a factor of 2, and an upside down flip. at front means a vertical stretch by a factor of 2, and an upside down flip.
The 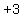 at the end means a shift up by 3 units. at the end means a shift up by 3 units.

If my function were  , I would use algebra to re-write it a way I like better: , I would use algebra to re-write it a way I like better:
 --> -->  --> -->  --> -->  . .
Then I would say the transformations from  are: are:
a  unit shift to the left, unit shift to the left,
a vertical stretch by a factor of 20, and
a shift up by 8 units.
Someone else may say that there was a horizontal shrinking by a factor of 2 and a vertical stretching by a factor of 5, but those two changes compound into the vertical stretch by a factor of 20 I listed. It is different ways to state the same thing.
IF MORE ALGEBRA KNOWLEDGE IS TO BE USED:
If someone gave me something like  I might think of foiling, I might think of foiling,
but I would not need to do that.
I know that, with zeros (x-intercepts) at  and and  , ,
the vertex and axis of a symmetry of that quadratic function is halfway between the zeros, at  . .
At that point,  . .
That, and the  in front, tells me that in front, tells me that  is is  transformed by transformed by
a  unit shift right, unit shift right,
a  unit shift down, and unit shift down, and
a vertical stretch by a factor of  . .
If someone was mean enough to give me something like  , I would "complete the square" as follows. , I would "complete the square" as follows.








That function is  transformed by transformed by
a  unit shift right, unit shift right,
a  unit shift down, and unit shift down, and
a vertical stretch by a factor of  . .
|
|
|
| |