SOLUTION: Consider the infinite geometric series n=1 up to infinitey then the equation is -4(1/3)^n-1 a. write the first four terms of the series b. does the series diverge or converg

Algebra ->  Sequences-and-series -> SOLUTION: Consider the infinite geometric series n=1 up to infinitey then the equation is -4(1/3)^n-1 a. write the first four terms of the series b. does the series diverge or converg      Log On


   

Question 83773: Consider the infinite geometric series
n=1 up to infinitey then the equation is -4(1/3)^n-1

a. write the first four terms of the series
b. does the series diverge or converge?
c. If the series has a sum, find the sum
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
In order to find the terms of the series sum%28+-4%281%2F3%29%5E%28n-1%29%2C+n=1%2C+infinity+%29 we need to find the terms of the sequence -4%281%2F3%29%5E%28n-1%29 first.

If we start at n=1, our first number of the sequence is
-4%281%2F3%29%5E%281-1%29=-4%281%2F3%29%5E0=-4
If we let n=2, our second number of the sequence is
-4%281%2F3%29%5E%282-1%29=-4%281%2F3%29%5E1=-4%2F3
If we let n=3, our third number of the sequence is
-4%281%2F3%29%5E%283-1%29=-4%281%2F3%29%5E2=-4%2F9
If we let n=4, our fourth number of the sequence is
-4%281%2F3%29%5E%284-1%29=-4%281%2F3%29%5E3=-4%2F27
If we let n=5, our fifth number of the sequence is
-4%281%2F3%29%5E%285-1%29=-4%281%2F3%29%5E4=-4%2F729
If we let n=6, our sixth number of the sequence is
-4%281%2F3%29%5E%286-1%29=-4%281%2F3%29%5E5=-4%2F59049
and so on...



a. write the first four terms of the series
Now that we've generated the sequence of numbers, lets generate the series

So now lets add up the individual terms of the sequence we found earlier
Sum of the first 2 terms of the sequence is
-4+%2F+1%2B-4+%2F+3=-16+%2F+3=-5.33333333333333
Sum of the first 3 terms of the sequence is
-4+%2F+1%2B-4+%2F+3%2B-4+%2F+9=-52+%2F+9=-5.77777777777778
Sum of the first 4 terms of the sequence is
-4+%2F+1%2B-4+%2F+3%2B-4+%2F+9%2B-4+%2F+27=-160+%2F+27=-5.92592592592593
Sum of the first 5 terms of the sequence is
-4+%2F+1%2B-4+%2F+3%2B-4+%2F+9%2B-4+%2F+27%2B-4+%2F+81=-484+%2F+81=-5.97530864197531


So the first four terms are

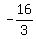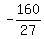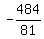
-16%2F3,-52%2F9,-160%2F27, -484%2F81

b. does the series diverge or converge?
If we let the series go on long enough, the series will converge. It's hard to see with the fractions, but the decimal values are clear enough. The series goes
-5.3333333333333 , -5.77777777777778 , -5.92592592592593 , -5.97530864197531...
where the 11th term is -5.99989838947315 and the 32th term is -5.99999999999999. So the series converges to -6.

c. If the series has a sum, find the sum

To find the sum of an infinite series, use this formula

S=a%2F%281-r%29 where S is the sum, a is the first term (in this case -4) and r is the ratio (in this case 1%2F3)

S=-4%2F%281-1%2F3%29 plug in a=-4 and r=1%2F3

S=-4%2F%283%2F3-1%2F3%29 Make 1 into an equivalent fraction with a denominator of 3

S=-4%2F%282%2F3%29 Combine the fractions in the denominator

S=%28-4%2F1%29%2A%283%2F2%29 Multiply the fractions by multiplying the first fraction by the reciprocal of the second

S=-12%2F2 Multiply

S=-6 Reduce

So the infinite sum converges to -6