Question 837553: The mean of a thirteen-item data set is 320. Eleven of the items are 300, 320, 199, 175, 325, 520, 156, 225, 326, 421, 504. The median is 325. Find the remaining two items in the set knowing these items have the greatest possible difference?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The mean of a thirteen-item data set is 320.
Eleven of the items are 300, 320, 199, 175, 325, 520, 156, 225, 326, 421, 504.
The median is 325.
Find the remaining two items in the set knowing these items have the greatest possible difference?
:
Let x = the sum of the remaining two items
:
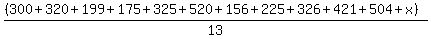 = 320 = 320
Add 'em, mult both sides by 13
3471 + x = 4160
x = 4160-3471
x = 689
Put the two values as as far as possible from the median, 325.
689-325 = 364
364/2 = 182
325 - 182 = 143 is the one remaining value
and
325 + 182 = 507 is the other remaining value
|
|
|