SOLUTION: a box contains 6 identical red balls, 3 identical white balls and 5 identical black balls. 3 balls are taken out from the box one after another without replacement. what the probab

When you see the words "at least one", it is always easier
to use the complement event because it's shorter than the
direct method.

The complement event of "the event that one ball is white" is the
event that "NO ball is white".

We calculate the probability of the complement event and then subtract
that probability from 1.

P(no ball is white) = P(choosing 3 from the 11 non-white balls from the 14 balls) =  = .

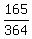Then we subtract from 1. .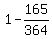

-------------------------

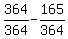
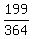The longer direct way is

P(exactly 1 white ball) + P(exactly 2 white balls) + P(exactly 3 white balls) =



 = .

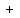
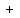
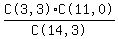
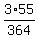
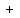
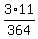
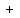
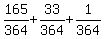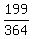This is longer but gives the exact same answer.  It shows that it is possible
to do "at least one" problems directly, but it is longer.  In many cases it is
much much longer.  For suppose there were 100 white balls!  The bottom line is
if you see "at least one", find the probability of the complement event and
subtract from 1.

Edwin