Question 83586: Help Please.
determine whether each of the following trinomials is a perfect square. If it is, factor the trinomials.
x^2-24x+48
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Is:
.
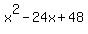
.
a perfect square? The answer is, "No, it is not."
.
But how do you easily get that answer. The method to use is called "Completing the Square."
.
How do you use that method? First, make sure that the coefficient of the  term term
is 1. [In this case it is, otherwise you would have to factor out from all the terms in
the trinomial the coefficient (multiplier) of the  term.] term.]
.
Next, forget about the +48 for the time being. Take half of the multiplier of the x term. That
multiplier is -24 and half of it is -12. Then square the -12 to get + 144.
.
Now we can say that 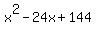 is the perfect square trinomial. [Its equivalent is the perfect square trinomial. [Its equivalent
form is 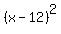 .] So for the given trinomial to be a perfect square, the +48 would .] So for the given trinomial to be a perfect square, the +48 would
have to be changed to +144.
.
Another way to do this (maybe even easier) is to use the discriminant of the quadratic
formula. The quadratic formula applies to all equations of the general form:
.

.
The discriminant of this equation is given by 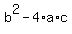 . If the discriminant . If the discriminant
is equal to zero, the trinomial is a perfect square (the equation has two real and
equal roots).
.
By comparing your problem with the general form of the quadratic equation you can see
that a = 1, b = -24, and c = +48. Substituting these values into the discriminant,
you get:
.
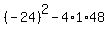
.
This simplifies to:
.

.
Since the discriminant does not equal zero, the given trinomial is not a perfect square.
.
However, suppose that the given trinomial had been 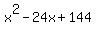 . In this case . In this case
a = 1, b = -24, and c = 144.
.
Substitute these values into the discriminant and you get:
.

.
And since the discriminant now equals zero, this trinomial is a perfect square. [As we
noted earlier the trinomial 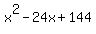 is equivalent to is equivalent to 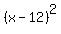 .] .]
.
Hope these couple of ways help you to understand your problem better.
|
|
|