There are two solutions, a big circle and very small one. We'll
have to do them separately because the y-coordinate of the center
of the big circle is positive and is the same as the radius,
whereas the y-coordinate of the center of the small circle is
negative and therefore the negative of its radius.
 Since the circle is tangent to the x-axis at (4,0), we know
that the center (h,k) is on the red vertical line x=4, and
so h=4.
For the big circle, the radius r is the same as k. So the
center is (4,r). We also know that the radius is the
perpendicular distance from the center to the given line.
The perpendicular distance from the point (x1,y1)
to the line Ax+y+C=0 is
d =
Since the circle is tangent to the x-axis at (4,0), we know
that the center (h,k) is on the red vertical line x=4, and
so h=4.
For the big circle, the radius r is the same as k. So the
center is (4,r). We also know that the radius is the
perpendicular distance from the center to the given line.
The perpendicular distance from the point (x1,y1)
to the line Ax+y+C=0 is
d = 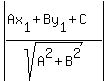 The given line is
3x-4y-17=0, so A=3, B=-4, C=-17, and the distance d
is the radius r, and the point (x1,y1) = (4,r),
the center of the circle.
r =
The given line is
3x-4y-17=0, so A=3, B=-4, C=-17, and the distance d
is the radius r, and the point (x1,y1) = (4,r),
the center of the circle.
r =  r =
r = 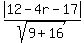 r =
r = 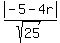 r =
r = 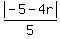 5r = |-5-4r|
Square both sides:
(5r)² = (|-5-4r|)²
25r² = 25+40r+16r²
9r²-40r-25 = 0
(9r+5)(r-5) = 0
r = -
5r = |-5-4r|
Square both sides:
(5r)² = (|-5-4r|)²
25r² = 25+40r+16r²
9r²-40r-25 = 0
(9r+5)(r-5) = 0
r = -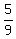 ; r=5
We ignore the negative solution.
So the equation of the big circle is
(x-h)² + (y-k)² = r²
(x-4)² + (y-5)² = 5²
(x-4)² + (y-5)² = 25.
---------------------------
For the little circle, since it's so tiny, we
need to zoom in on it:
; r=5
We ignore the negative solution.
So the equation of the big circle is
(x-h)² + (y-k)² = r²
(x-4)² + (y-5)² = 5²
(x-4)² + (y-5)² = 25.
---------------------------
For the little circle, since it's so tiny, we
need to zoom in on it:
 For the little circle, k, the y-coordinate of the center, is
below the x-axis and is negative. Therefore k = -r, whereas
in the big circle k and r were equal. So the radius r of the
the little circle is -k. So k = -r, and the center is (4,-r).
As before we know that the radius is the perpendicular
distance from the center (4,-r)to the given line.
The perpendicular distance from the point (x1,y1)
to the line Ax+y+C=0 is
d =
For the little circle, k, the y-coordinate of the center, is
below the x-axis and is negative. Therefore k = -r, whereas
in the big circle k and r were equal. So the radius r of the
the little circle is -k. So k = -r, and the center is (4,-r).
As before we know that the radius is the perpendicular
distance from the center (4,-r)to the given line.
The perpendicular distance from the point (x1,y1)
to the line Ax+y+C=0 is
d = 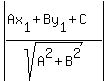 The given line is
3x-4y-17=0, so as before A=3, B=-4, C=-17, and the distance d
is the radius r, but this time the point (x1,y1) = (4,-r),
the center of the little circle.
r =
The given line is
3x-4y-17=0, so as before A=3, B=-4, C=-17, and the distance d
is the radius r, but this time the point (x1,y1) = (4,-r),
the center of the little circle.
r = 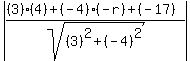 r =
r = 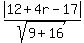 r =
r =  r =
r =  5r = |-5+4r|
Square both sides:
(5r)² = (|-5+4r|)²
25r² = 25-40r+16r²
9r²+40r-25 = 0
(9r-5)(r+5) = 0
r =
5r = |-5+4r|
Square both sides:
(5r)² = (|-5+4r|)²
25r² = 25-40r+16r²
9r²+40r-25 = 0
(9r-5)(r+5) = 0
r = 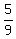 ; r = -5
We ignore the negative answer.
So the equation of the little circle is
(x-h)² + (y-k)² = r²
(x-4)² + (y-
; r = -5
We ignore the negative answer.
So the equation of the little circle is
(x-h)² + (y-k)² = r²
(x-4)² + (y-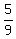 )² =
)² = 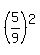 (x-4)² + (y-
(x-4)² + (y-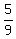 )² =
)² = 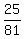 .
Edwin
.
Edwin