Question 83553: I am asking someone to please help me with my last 2 problems for my final which has to be in before 12 midnight. I do not understand what to do with
either one of these problems. Thanking you in advance.
solve the following system of linear inequalities by graphing.
3x+4y<12
x+3y<6
y>0
give the coordinates of the point graphed.\
A)(-3,2)
B)(2,-3)
C)(3,-2)
D) (-2,3)
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 3x+4y<12
x+3y<6
y>0
give the coordinates of the point graphed.\
A)(-3,2)
B)(2,-3)
C)(3,-2)
D) (-2,3)
----------------
3x+4y<12
x+3y<6
y>0
---------
Solve each for y as follows:
y < (-3/4)y + 3
y < (-1/3)x + 2
y > 0
---------------
Graph the EQUALITIES associated with these INEQUALITIES:
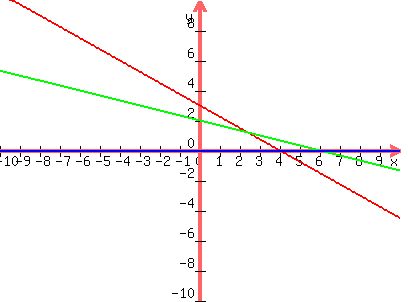
---------------
Find the half plane graph of each of the INEQUALITIES.
------------
Find the intersection of those half-planes.
That is the solution set of the system on INEQUALITIES.
=============
Comment: Your 2nd question cannot be answered without see the point
you are describing.
================
Cheers,
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! SOLUTION BY EDWIN McCRAVY
I am asking someone to please help me with my last 2 problems for my final which has to be in before 12 midnight. I do not understand what to do with
either one of these problems. Thanking you in advance.
solve the following system of linear inequalities by graphing.
3x+4y<12
x+3y<6
y>0
give the coordinates of the point graphed.
A)(-3,2)
B)(2,-3)
C)(3,-2)
D) (-2,3)
Plug each one into all the inequalities to see
if they are all true.
I'll skip around.
Let's try D first:
Substitute (x,y) = (-2,3)
Plug in 3x+4y < 12
3(-2) + 4(3) < 12
-6 + 12 < 12
6 < 12
That's true:
Plug in x+3y < 6
(-2) + 3(3) < 6
-2 + 9 < 6
7 < 6
Oh, oh, that's false. So the answer isn't (D).
Now let's try (B)
Substitute (x,y) = (2,-3)
Plug in 3x+4y < 12
3(2) + 4(-3) < 12
6 - 12 < 12
-6 < 12
That's true:
Plug in x+3y < 6
(2) + 3(-3) < 6
2 - 9 < 6
-7 < 6
That's true.
Plug in y > 0
-3 > 0
Oh, oh, that's false. So the answer isn't (B).
Now let's try (C)
Substitute (x,y) = (3,-2)
Plug in 3x+4y < 12
3(3) + 4(-2) < 12
9 - 8 < 12
1 < 12
That's true:
Plug in x+3y < 6
(3) + 3(-3) < 6
3 - 9 < 6
-3 < 6
That's true.
Plug in y > 0
-2 > 0
Oh, oh, that's false. So the answer isn't (C).
So let's try (A).
Let's see:
Substitute (x,y) = (-3,2)
Plug in 3x+4y < 12
3(-3) + 4(2) < 12
-9 + 8 < 12
-1 < 12
That's true:
Plug in x+3y < 6
(-3) + 3(2) < 6
-3 + 6 < 6
3 < 6
That's true.
Plug in y > 0
2 > 0
That's true. So they are all true! So that
means (x,y) = (-3,2) is the only one of the
4 that satisfies all three of the given
inequalities,making the correct choice (A).
Edwin
|
|
|