Question 835252: write the polynomial function
f(x)= x^5+x^3+2x^2-12x+8
as the product of linear factors
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
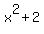 is not a linear factor. is not a linear factor.
It is a quadratic polynomial, and can only be factored using imaginary numbers.
HOW DO WE GET THAT?
Noticing that  , ,
we realize that  is a factor of is a factor of  . .
Dividing, we find that

Since  , ,
 must be a factor of must be a factor of  . .
Dividing, we find that
 . .
So  and and  , ,
which means that

At this point, either we may realize that 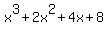 is zero for is zero for  , ,
or we may realize that 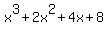 is divisible by is divisible by  . .
In either case we divide and find that  . .
So, putting it all together,
 . .
Alternatively, we may realize that

and since  , ,
dividing both sides by  we conclude that we conclude that

|
|
|