For limits of rational expressions, i.e. "
"
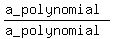1. Substitute what x approaches. If the denominator is not 0.
what you get is the answer, and you're done.
2. If the denominator is 0, and the numerator is not 0, then the
answer is 
if the numerator is positive and 
if the numerator is negative, and you're done.
3. If the numerator is also 0, factor numerator and denominator and
cancel all common factors.
4. Substitute what x approaches, simplify, and what you get is the answer.
------------------------
1. 
. Both
numerator and denominator are 0, so we go to step 3.
3. Factor the numerator: Candidates for zeros are ±1,±2
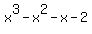has 1 sign change, so it has one
positive zero. We try 1:
1|1 -1 -1 -2
| 1 0 -1
1 0 -1 -3 So 1 is not a zero
We try 2
2|1 -1 -1 -2
| 2 2 2
1 1 1 0 So 2 is a zero, so the numerator factors
as (x-2)(x²+x+1)
The denominator x²-6x+8 factors as (x-2)(x-4)
So we have:
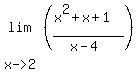
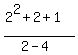
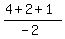
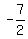You do the other one. The answer is 
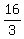Edwin
