|
Question 834912: Find the equation of the circle tangent to x=0; center on x+y=10; contains (2,9)
Answer by reviewermath(1029)   (Show Source): (Show Source):
You can put this solution on YOUR website! Q:
Find the equation of the circle tangent to x=0; center on x+y=10; contains (2,9)
------------------------------------------------------------
A:
Let (h, k) be the center and r the radius of the circle.
The center lies on the line x + y = 10, so h + k = 10 or h = 10 - k.
The distance between the line x = 0 and the center (h, k) is h or 10 - k.
The distance between (h, k) and (2, 9) is equal to
 , substitute h = 10 - k , substitute h = 10 - k
= 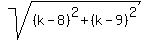
The two distances are equal (both are equal to the length of the radius).
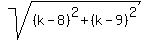 = 10 - k, square both sides = 10 - k, square both sides


(k - 5)(k - 9) = 0
k = 5 or 9
If k = 5:
then h = 10 - 5 = 5, so the center is (5, 5) and the radius is r = 5.
The equation is 
If k = 9:
then h = 10 - 9 = 1, so the center is (1, 9) and the radius is r = 1.
The equation is 
Graph:

Answers: 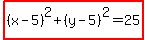 or or 
|
|
|
| |