Question 834608: "Going into the final exam, which counts as two grades, Kendra has test scores of 84, 78,64, and 88. What score does Kendra need on the final exam in order to have an average of 80?"
I always have a problem with these questions.
I don't want to know the answer cause I want to work it for myself, I just want to know how to set up the problem so I can do it for similar problems in the future too.
Answer by LinnW(1048)   (Show Source): (Show Source):
You can put this solution on YOUR website! For the tests with grades
84, 78, 64, and 88 each test has a weighting of 1.
The final has a weighting of 2.
set w1 = the first weight
w2 = the second weight
w3 = the third weight
and so forth.
set g1 = the first grade
g2 = the second grade
g3 = the third grade
and so forth.
We are looking for a weighted average.
((w1)(g1) + (w2)(g2) + ... )/(sum of weights)
In our situation, g1 = 84, g2 = 78, g3 = 64, g4 = 88 and
g5 = unknown ( This is the final. ).
w1 = 1 , w2 = 1, w3 = 1, w4 = 1, w5 = 2
For our problem we have
((1)(84) + (1)(78) + (1)(64) + (1)(88) + (2)(g5))/(sum of the weights)
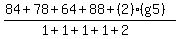


To simplify use x in place of g5

Set this equal to 80.

Multiply each side by 6


add -314 to each side



We need a grade of 83 on the final to obtain an average of 80 .
|
|
|