Question 834474: Find all real zeros:

Thanks for the help!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
The possible rational zeros can be written as  or or 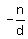 where where  is a factor of is a factor of  and and  is a factor of is a factor of 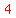 . .
They are:
-6,-3,-2,-1,1,2,3,6,
-3/2,-3/4,-1/2,-1/4,1/4,1/2,3/4,3/2.
Trying the easiest ones first, we find two zeros:





Since  and and  , ,
 and and  are factors of are factors of  . .
So, we can divide  by by  and by and by  one after the other, one after the other,
or we can divide  by by  . .
Either way, the final quotient is  , ,
which has  as a double zero. as a double zero.
So  , and the zeros of , and the zeros of  are are
 , ,  , and , and  . .
|
|
|